2022-2023学年山东省日照实验高级中学高三（上）段考数学试卷（10月份）（一）

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中只有一项是符合题目要求的.

• 1．已知集合A={x|x（x-2）≤0}，B={x|0＜x≤1}，则A∩B=（　　）

  A．{x|0≤x≤1}

  B．{x|0＜x≤1}

  C．{x|0＜x≤2}

  D．∅
  组卷：77引用：6难度：0.9

  解析

• 2．若复数z满足（1+i）z=|1+i|，则z的虚部为（　　）

  A． - 2 i

  B． - 2

  C． - 2 2 i

  D． - 2 2
  组卷：38引用：10难度：0.9

  解析

• 3．已知角α的顶点在坐标原点，始边与x轴正半轴重合，终边经过点

  P

  （

  -

  2

  ，

  1

  ）

  ，则cos2α=（　　）

  A． 2 2 3

  B． 1 3

  C． - 1 3

  D． - 2 2 3
  组卷：324引用：10难度：0.8

  解析

• 4．函数

  y

  =

  ln

  （

  x

  +

  x

  2

  +

  1

  ）

  •

  cos

  2

  x

  的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：280引用：7难度：0.8

  解析

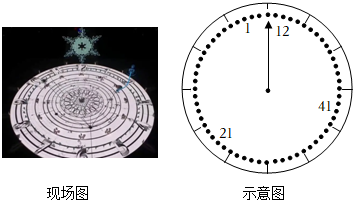• 5．冬残奥会闭幕式上，中国式浪漫再现，天干地支时辰钟表盘再现，由定音鼓构成的“表盘”形象上，60名残健共融表演者用行为模拟“指针”每圈60个时间刻度的行进轨迹．若以图中12点与圆心连线为始边，某时刻指向第1，21，41名残健共融表演者的“指针”为终边的角分别记为α，β，γ，则cosα+cosβ+cosγ的值为（　　）

  A．-1

  B．0

  C．1

  D．cosα
  组卷：64引用：6难度：0.7

  解析

• 6．已知a=

  e

  -

  2021

  2022

  ，b=

  1

  2022

  ，c=

  ln

  2023

  2022

  ，则a,b,c的大小关系为（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．c＞a＞b

  D．b＞c＞a
  组卷：170引用：7难度：0.7

  解析

• 7．已知f（x）是R上的奇函数，f（1+x）=f（1-x），当x₁，x₂∈[0，1]，且x₁≠x₂时，

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ＞0，则当-3≤x≤1时，不等式xf（x）＞0的解集为（　　）

  A．[-1，0）∪（0，1]	B．[-3，-2）∪（0，1]
  C．（-2，-1）∪（0，1]	D．（-2，0）∪（0，1]
  组卷：227引用：3难度：0.5

  解析

四、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.

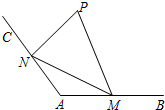• 21．如图，为方便市民游览市民中心附近的“网红桥”，现准备在河岸一侧建造一个观景台P，已知射线AB，AC为两边夹角为120°的公路（长度均超过3千米），在两条公路AB，AC上分别设立游客上下点M，N，从观景台P到M，N建造两条观光线路PM，PN，测得AM=

  3

  千米，AN=

  3

  千米．
  （1）求线段MN的长度；
  （2）若∠MPN=60°，求两条观光线路PM与PN所围成△PMN的面积的最大值．
  组卷：62引用：3难度：0.7

  解析

• 22．已知f（x）=4x-alnx-

  1

  2

  x

  2

  -2有两个极值点x₁，x₂（x₁＜x₂）．
  （1）求实数a的取值范围；
  （2）证明：f（x₁）+f（x₂）＜6-lna.
  组卷：108引用：5难度：0.4

  解析