2022-2023学年山东省烟台市招远市六年级（下）期中数学试卷（五四学制）

一．选择题（本大题共10个小题，每小题3分，满分30分）

• 1．下列四个生产生活现象，可以用“两点之间线段最短”来解释的是（　　）

  A．用两颗钉子可以把木条固定在墙上

  B．在高速公路的建设中，通常从大山中开挖隧道穿过，把道路取直，以缩短路程

  C．植树时，只要定出两棵树的位置，就能使同一行树坑在一条直线上

  D．打靶的时候，眼睛要与枪上的准星、靶心在同一直线上
  组卷：909引用：9难度：0.8

  解析

• 2．下列计算错误的有（　　）
  ①（3xy²）³=27x³y⁶；
  ②（-a^2m）³=a^6m；
  ③x¹²÷x⁴=x³；
  ④2x³•3x⁴=6x¹²．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：650引用：2难度：0.5

  解析

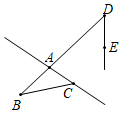• 3．如图，下列说法中正确的是（　　）

  A．直线AC在线段BC上

  B．射线DE与直线AC没有公共点

  C．直线AC与线段BD相交于点A

  D．点D在直线AC上
  组卷：204引用：2难度：0.8

  解析

• 4．在下列多项式乘法中，可以用平方差公式计算的是（　　）

  A．（-2a+3b）（-3b-2a）	B．（2a-3b）（-2a+3b）
  C．（a+1）（-a-1）	D．（a2-b）（a+b2）
  组卷：235引用：2难度：0.5

  解析

• 5．已知本学期某学校下午上课的时间为14时20分，则此时刻钟表上的时针与分针的夹角为_____度．（　　）

  A．40°

  B．50°

  C．60°

  D．70°
  组卷：267引用：3难度：0.6

  解析

• 6．如果多项式4x²-（a-1）x+9是一个完全平方式，则a的值是（　　）

  A．±6

  B．7或-5

  C．13或-11

  D．±12
  组卷：968引用：4难度：0.5

  解析

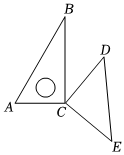• 7．如图，是直角顶点重合的一副三角板，若∠BCD=40°，下列结论错误的是（　　）

  A．∠ACD=130°	B．∠ACD=∠BCE
  C．∠ACE=130°	D．∠ACE-∠BCD=100°
  组卷：593引用：6难度：0.5

  解析

• 8．若a=0.4²，b=-4^-2，

  c

  =

  （

  -

  1

  4

  ）

  -

  2

  ，

  d

  =

  （

  -

  1

  4

  ）

  0

  ，则（　　）

  A．b＜a＜c＜d

  B．b＜a＜d＜c

  C．c＜d＜a＜b

  D．c＜a＜d＜b
  组卷：1083引用：4难度：0.5

  解析

三．解答题（本大题共9个小题，共72分，请在答题卡指定区域做题）

• 24．代数推理：
  

  例题：求x2+8x+21的最小值． 解：x2+8x+21 =x2+2x•4+42-42+21 =（x+4）2+5． 无论x取何值，（x+4）2总是非负数， 即（x+4）2≥0， 所以（x+4）2+5≥5． 所以当x=-4时，x2+8x+21有最小值，最小值为5．

  阅读材料：利用完全平方式，将多项式x²+bx+c变形为（x+m）²+n的形式，然后由（x+m）²≥0就可以求出多项式x²+bx+c的最小值．
  根据上述材料，解答下列问题：
  （1）填空：x²-12x+

  =（x-

  ）²；
  （2）将多项式x²+16x-1变形为（x+m）²+n的形式，并求出x²+16x-1的最小值；
  （3）若一个长方形的长和宽分别为（2a+3）和（3a+5），面积记为S₁，另一个长方形的长和宽分别为5a和（a+3），面积记为S₂，试比较S₁和S₂的大小，并说明理由．
  组卷：692引用：8难度：0.5

  解析

• 25．学习材料：
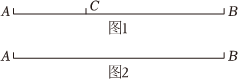
  如图1，点C在线段AB上，图中有三条线段，分别为线段AB，AC和BC，若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．
  解决问题：
  （1）线段的中点

  这条线段的“巧点”，线段的三等分点

  这条线段的“巧点”（填“是”或“不是”）；
  （2）若线段AB=18cm,点C为线段AB的“巧点”，则AC=

  ；
  （3）如图2，已知AB=18cm,动点P从点A出发，以2cm/s的速度沿AB向点B运动，点Q从点B出发，以1cm/s的速度沿BA向点A运动，点P、Q同时出发，当其中一点到达终点时，运动停止，设运动的时间为t秒，当t为何值时，点P为线段AQ的“巧点”？并说明理由．
  组卷：268引用：3难度：0.5

  解析