2022-2023学年四川省成都市锦江区嘉祥外国语高级中学高一（下）月考数学试卷（3月份）

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知角α的终边经过点P（-3，4），则sinα的值等于（　　）

  A．- 3 5

  B． 3 5

  C． 4 5

  D．- 4 5
  组卷：720引用：24难度：0.9

  解析

• 2．已知

  AB

  =（3，5），

  AC

  =（-1，2），则

  CB

  =（　　）

  A．（4，3）

  B．（-4，-3）

  C．（-4，3）

  D．（4，-3）
  组卷：525引用：7难度：0.8

  解析

• 3．sin40°cos10°-sin130°sin10°等于（　　）

  A．- 3 2

  B． 3 2

  C．- 1 2

  D． 1 2
  组卷：195引用：7难度：0.7

  解析

• 4．函数f（x）=

  xsinx

  2

  |

  x

  |

  -

  1

  的大致图象为（　　）

  A．	B．
  C．	D．
  组卷：196引用：2难度：0.8

  解析

• 5．已知|

  a

  |=4，|

  b

  |=2，当

  a

  与

  b

  的夹角为

  π

  3

  时，

  a

  在

  b

  上的投影向量为（　　）

  A．2

  B． b

  C．2 3

  D． 3   b
  组卷：209引用：6难度：0.9

  解析

• 6．已知tanα=2，则

  sinα

  -

  si

  n

  3

  α

  sin

  （

  α

  +

  π

  2

  ）

  =（　　）

  A． 3 5

  B． 2 5

  C． - 2 5

  D． - 3 5
  组卷：150引用：1难度：0.8

  解析

• 7．已知

  -

  π

  2

  ＜

  θ

  ＜

  π

  2

  ，且

  sin

  （

  θ

  -

  π

  6

  ）

  =

  1

  3

  ，则sinθ的值为（　　）

  A． 1 6

  B． 2 2 6

  C． 2 - 3 6

  D． 3 + 2 2 6
  组卷：166引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

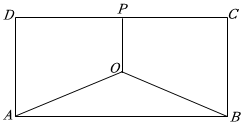• 21．为了给师生提供更好的就餐环境，嘉祥锦江校区对食堂进行改造升级，其中为一项为更新供水系统如图是供水系统设计图纸的一部分，三个用水点分别位于矩形ABCD的两个顶点A、B及CD的中点P处，AB=30m,BC=15m,为了给三个用水点供水，现要在该矩形区域上（含边界）一点O处，建造一个供水点，并铺设三条供水管道AO、BO、PO．
  （1）若要使点O在以AB为直径的半圆弧上，求铺设两条管道AO，BO长度的和L的最大值；
  （2）若要使点O与A、B等距离，求铺设三条管道AO、BO、PO长度的和S的最小值，并求此时PO的长度．
  组卷：16引用：1难度：0.6

  解析

• 22．设 f（x）=sinⁿx+cosⁿx,n∈{n|n=2k,k∈N₊}．
  （1）当k=1且x∈R时，求f（x）的值；
  （2）当k=2且x∈R时，求f（x）的值域，说明理由；当k=2023且x∈R时，猜想f（x）的值域，不需证明；
  （3）当k=2时，将f（x）的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图象对应的函数记作y=g（x），设h（x）=af（x-

  π

  8

  ）-|g（x-

  π

  4

  ）-g（x）|，当x∈[-

  3

  π

  8

  ，

  π

  4

  ]时，求h（x）的零点个数．
  组卷：29引用：1难度：0.5

  解析