当前位置：试卷中心 > 试卷详情

2021-2022学年浙江省舟山市定海二中等四校联考九年级（下）第二次质检数学试卷

发布：2024/7/13 8:0:9

一、选择题（本题有10小题，每小题3分，共30分）

1．-2023表示（　　）
A．2023的绝对值 B．2023的倒数
C．-2023的相反数 D．2023的相反数
组卷：3引用：1难度：0.8
解析
2．下列四个几何体中，主视图是三角形的是（　　）
A． B． C． D．
组卷：211引用：41难度：0.9
解析
3．2023年，我国将全面推进探月工程，规划包括嫦娥六号、嫦娥七号和嫦娥八号任务，已知月球与地球的平均距离约为384000000米，数据384000000用科学记数法表示为（　　）
A．0.384×10⁹ B．3.84×10⁸ C．38.4×10⁷ D．384×10⁶
组卷：336引用：15难度：0.8
解析
4．下列能说明命题“若a＞b,则a²＞b²”是假命题的反例是（　　）
A．a=-1，b=0 B．a=-1，b=-1 C．a=-1，b=-2 D．a=2，b=1
组卷：250引用：7难度：0.7
解析
5．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）
A．30° B．25° C．20° D．15°
组卷：3687引用：256难度：0.9
解析
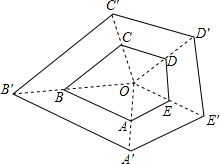6．如图，五边形ABCDE与五边形A′B′C′D′E′是位似图形，O为位似中心，OD=
1
2
OD′，则A′B′：AB为（　　）
A．2：3 B．3：2 C．1：2 D．2：1
组卷：415引用：29难度：0.7
解析
7．圆锥的底面半径为4，侧面展开图扇形的圆心角为120°，则该圆锥的母线长为（　　）
A．6 B．12 C．18 D．24
组卷：126引用：2难度：0.7
解析
8．《孙子算经》是南北朝时期重要的数学专著，包含“鸡兔同笼”等许多有趣的数学问题．如：“今有木，不知长短，引绳度之，余绳四尺五寸：屈绳量之，不足一尺．木长几何？”大意是：“用一根绳量一根木，绳剩余4.5尺；将绳对折再量木，木剩余1尺．问木长多少？”设木长x尺，绳长y尺，则依题意可列方程组（　　）
A．
y
=
x
+
4
.
5
y
=
2
x
-
1
B．
y
=
x
-
4
.
5
y
=
2
x
-
1
C．
y
=
x
-
4
.
5
0
.
5
y
=
x
+
1
D．
y
=
x
+
4
.
5
0
.
5
y
=
x
-
1
组卷：342引用：11难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题有8小题，共66分）

23．若关于x的函数y,当
t
-
1
3
≤
x
≤
t
+
1
3
时，函数y的最大值为M，最小值为N，令函数
h
=
M
-
N
2
，我们不妨把函数h称之为函数y的“联合函数”．
（1）若函数y=6x,当t=1时，求函数y的“联合函数”h的值；
（2）若函数
y
=
3
x
（x≥1），求函数y的“联合函数”h的解析式及h的最大值；
（3）若函数y=-x²+4x+c,是否存在实数c,使得函数y的最大值等于函数y的“联合函数”h的最小值．若存在，求出c的值；若不存在，请说明理由．
组卷：104引用：1难度：0.3
解析
24．已知，在△ABC中，∠ACB=90°，BC=8，以BC为直径的⊙O与AB交于点H，将△ABC沿射线AC平移得到△DEF，连接BE．

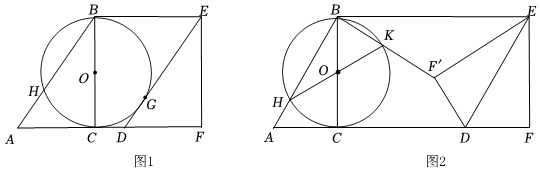
（1）如图1，DE与⊙O相切于点G．
①求证：四边形BCFE是矩形；
②求EG•DG的值；
（2）如图2，延长HO与⊙O交于点K，将ADEF沿DE折叠，点F的对称点F'恰好落在射线BK上．
①猜想HK与EF'的关系，请说明理由；
②若KF'=4，求平移的距离．
组卷：12引用：1难度：0.4
解析