已知，在△ABC中，∠ACB=90°，BC=8，以BC为直径的⊙O与AB交于点H，将△ABC沿射线AC平移得到△DEF，连接BE．
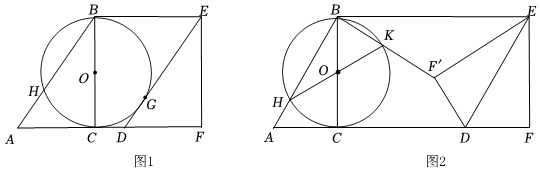
（1）如图1，DE与⊙O相切于点G．
①求证：四边形BCFE是矩形；
②求EG•DG的值；
（2）如图2，延长HO与⊙O交于点K，将ADEF沿DE折叠，点F的对称点F'恰好落在射线BK上．
①猜想HK与EF'的关系，请说明理由；
②若KF'=4，求平移的距离．
【考点】圆的综合题．
【答案】（1）①证明见解析；
②16；
（2）①HK∥EF'；理由见解析；
②．
②16；
（2）①HK∥EF'；理由见解析；
②
20
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：12引用：1难度：0.4
相似题
-
1．在⊙O中，直径AB与弦CD（非直径）交于点E，DE=CE，弦BG⊥BC交⊙O于点G，交CD于点F．
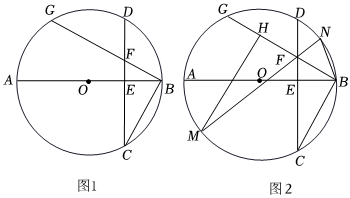
（1）如图1，求证：∠ABF=∠BCD；
（2）如图2，点N为弧BD上一点，连接BN、NF，并延长NF交⊙O于点M，H为FG上一点，连接MH，BN=BF，∠HMF=∠HBN，求证：FH=GH．12发布：2025/5/24 14:30:1组卷：107引用：1难度：0.1 -
2．【问题呈现】阿基米德折弦定理：阿基米德（archimedes,公元前287-公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，点M是
的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=DB+BA．下面是运用“截长法”证明CD=DB+BA的部分证明过程．ˆABC
证明：如图2，在CD上截取CG=AB，连接MA、MB、MC和MG．
∵M是的中点，ˆABC
∴MA=MC，
又∵∠A=∠C，BA=GC，
∴△MAB≌△MCG，
∴MB=MG，
又∵MD⊥BC，
∴BD=DG，
∴AB+BD=CG+DG即CD=DB+BA．
【理解运用】如图1，AB、BC是⊙O的两条弦，AB=4，BC=6，点M是的中点，MD⊥BC于点D，则BD=；ˆABC
【变式探究】如图3，若点M是的中点，【问题呈现】中的其他条件不变，判断CD、DB、BA之间存在怎样的数量关系？并加以证明．ˆAC
【实践应用】如图4，BC是⊙O的直径，点A圆上一定点，点D圆上一动点，且满足∠DAC=45°，若AB=6，⊙O的半径为5，则AD=．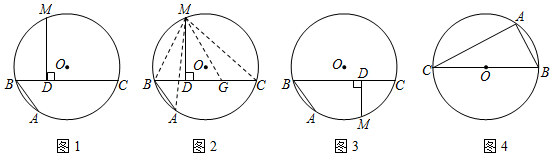
发布：2025/5/24 15:30:1组卷：1264引用：8难度：0.2 -
3．已知AP=d是半圆O的直径，点C是半圆O上的一个动点（不与点A、P重合），联结AC，以直线AC为对称轴翻折AO，将点O的对称点记为O1，射线AO1交半圆O于点B，连接OC．
（1）如图1，推断AB和OC位置关系；
（2）如图2，当点B与点O1重合时，用d表示弧PC的长；
（3）过点C作射线AO1的垂线，垂足为E，连接OE交AC于F．当d=10，O1B=1时，求的值．CFAF发布：2025/5/24 15:30:1组卷：57引用：1难度：0.3
