2023-2024学年重庆市九龙坡区铁路中学高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设

  a

  =

  （

  1

  ，

  y

  ,

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ，-

  1

  ）

  ，且

  a

  ⊥

  b

  ，则y等于（　　）

  A．-1

  B．1

  C．-2

  D．2
  组卷：60引用：4难度：0.8

  解析

• 2．已知点A（1，3），B（5，7），则线段AB的垂直平分线所在的直线方程为（　　）

  A．2x+y-5=0

  B．x+y-8=0

  C．x+2y+3=0

  D．x+y+6=0
  组卷：174引用：6难度：0.7

  解析

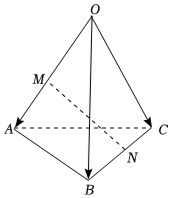• 3．如图，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M在

  OA

  上，且满足

  OM

  =2

  MA

  ，点N为BC的中点，则

  NM

  =（　　）

  A． 2 3 a - 1 2 b - 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 1 2 a - 2 3 b + 1 2 c
  组卷：366引用：15难度：0.7

  解析

• 4．直线y=x-1被椭圆2x²+y²=4所截得的弦的中点坐标是（　　）

  A． （ 1 3 ，- 2 3 ）

  B． （ - 2 3 ， 1 3 ）

  C． （ 1 2 ，- 1 3 ）

  D． （ - 1 3 ， 1 2 ）
  组卷：284引用：5难度：0.7

  解析

• 5．已知圆C过点A（7，-2），B（4，1），且圆心在x轴上，则圆C的方程是（　　）

  A．（x-5）2+y2=8	B．（x-6）2+y2=5
  C．（x-5）2+y2=4	D．（x-4）2+y2=13
  组卷：211引用：3难度：0.7

  解析

• 6．已知a、b、c成等差数列，则直线ax-by+c=0被曲线x²+y²-2x-2y=0截得的弦长的最小值为（　　）

  A． 2

  B．1

  C． 2 2

  D．2
  组卷：120引用：5难度：0.7

  解析

• 7．已知EF是棱长为8的正方体外接球的一条直径，点M在正方体表面上运动，则

  ME

  •

  MF

  的最小值为（　　）

  A．-48

  B．-32

  C．-16

  D．0
  组卷：193引用：12难度：0.7

  解析

四、解答题：本题共6个小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．如图，在多面体ABCDE中，平面ACD⊥平面ABC，BE⊥平面ABC，△ABC和△ACD均为正三角形，

  AC

  =

  2

  ，

  BE

  =

  3

  ，点M为线段CD上一点．
  （1）求证：DE⊥AM；
  （2）若EM与平面ACD所成角为

  π

  3

  ，求平面AMB与平面ACD所成锐二面角的余弦值．
  
  组卷：292引用：5难度：0.5

  解析

• 22．如图，椭圆

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  和圆

  C

  2

  ：

  x

  2

  +

  y

  2

  =

  b

  2

  ，已知圆C₂将椭圆C₁的长轴三等分，椭圆C₁右焦点到右顶点的距离为

  3

  -

  2

  2

  ，椭圆C₁的下顶点为E，过坐标原点O且与坐标轴不重合的任意直线l与圆C₂相交于点A，B．
  （1）求椭圆C₁的方程；
  （2）若直线EA，EB分别与椭圆C₁相交于另一个交点为点P，M，求证：直线PM经过定点．
  组卷：120引用：3难度：0.5

  解析