2021-2022学年河南省商丘市夏邑县八年级（下）期末数学试卷
发布：2024/6/30 8:0:9
一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的。
-
1．函数
中自变量x的取值范围是（ ）y=2x+1组卷：588引用：12难度：0.9 -
2．下列关于平行四边形的说法：①平行四边形的对角相等，邻角互补；②平行四边形既是中心对称图形，又是轴对称图形；③通过平行四边形对称中心的任意一条直线可以把平行四边形的面积等分；④平行四边形的两条对角线把平行四边形的面积四等分．其中错误的个数（ ）
组卷：17引用：2难度：0.7 -
3．数学老师计算同学们一学期的数学平均成绩时，将平时、期中、期末成绩按2：3：5的权重计算，若计算结果不是整数的按四舍五入保留整数．小华平时、期中、期末的数学成绩分别为90分、82分、85分，则小华这一学期的数学平均成绩（ ）
组卷：1引用：2难度：0.5 -
4．已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示（ ）
组卷：230引用：6难度：0.9 -
5．将x、y的值同时扩大到原来的10倍，则关于分式
的值，说法正确的是（ ）x+yxy组卷：24引用：3难度：0.5 -
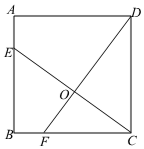6．如图，点E是正方形ABCD的边AB上任一点（不与顶点A、B重合），连结CE，过点D作DF⊥CE交BC于F，CE与DF交于点O．则下列说法：①△CBE≌△DCF；②AE=BF；③S四边形BFOE=S△COD；④S四边形ABFD=S四边形ADCE；⑤OE=OC．其中正确的个数是（ ）组卷：9引用：2难度：0.6 -
7．若点P（1-2t,t-3）位于第三象限，则t的取值范围是（ ）
组卷：11引用：2难度：0.5
-
22．实践与探究题
问题：直角三角形除了三边之间、两个锐角之间有特殊的关系外，斜边上的中线有什么性质呢？
丽丽同学利用直角三角形纸片进行了如下的折叠实验：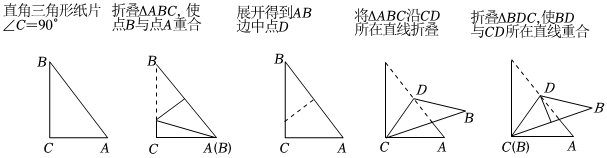
（1）观察发现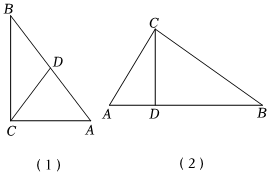
①观察丽丽同学的折叠实验，你发现线段CD与AB之间有何数量关系？在图（1）所示的Rt△ABC中，∠C=90°，CD是斜边AB上中线．请根据图（1）证明你的猜想．
②根据上面的探究，总结直角三角形斜边上的中线性质．
（2）拓展应用：如图（2），CD是Rt△ABC的斜边AB上的高，若CD=5，则Rt△ABC面积的最小值等于 ．组卷：189引用：4难度：0.5 -
23．阅读理解题．
先阅读下列内容，再完成后面的任务．
在数学探究课上，张老师出示了如下题目：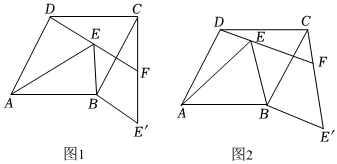
（1）问题1、如图1，四边形ABCD是菱形，∠DAB=60°，点E是菱形内的一动点，且∠AEB=60°，将△ABE绕点B顺时针旋转120°得到△CBE'，连接DE，并延长DE交CE'于F．如果∠ABE=90°，猜想四边形BE'FE为何特殊的平行四边形？并说明理由．
在同学们顺利地解答了问题1后，张老师又将该题做了如下的引申拓展：
（2）问题2、若问题1去掉条件“∠ABE=90°”，其它条件不变，如图2，上面结论是否还成立？若成立，请证明；若不成立，请说明理由．
经过同学们自探后，“追梦组”的同学们进行了讨论；
小菡：没有了∠ABE=90°这一条件了，应该上面的结论不成立了．
迎晖：观察图（2），猜想上面的结论还成立．
夏梅：上面的结论还成立，证明该结论成立的难点是如何证明∠BEF=60°．
迎晖：只要证明了∠AED=60°，就容易证得∠BEF=60°．后面的证明方法与问题1里的证明方法完全一样了．
……
突然，智明同学说我会证明了：连接BD，在线段AE上截取AH=BE，连接DH，就可以证得∠AED=60°．组里的同学们在智明的启发下，也顺利的解答问题2．
任务一：完整写出问题1的解答过程；
任务二：在问题2中证明∠BEF=60°（后面的证明不用写出来了！）．组卷：44引用：2难度：0.5
