2023-2024学年四川省广安市友谊中学高三(上)月考数学试卷(文科)(9月份)
发布:2024/8/15 17:0:2
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.若集合A={x|ln(x-1)<0},B={x|2x-3≥0},则A∩B=( )
组卷:50引用:3难度:0.8 -
2.若幂函数y=(m2-2m-2)xm-2在(0,+∞)递减,则m的值为( )
组卷:6引用:2难度:0.7 -
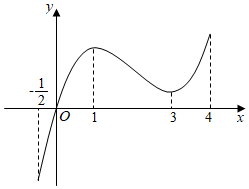 3.定义在区间上的函数f(x)的导函数f'(x)的图象如图所示,则下列结论正确的是( )[-12,4]组卷:581引用:8难度:0.7
3.定义在区间上的函数f(x)的导函数f'(x)的图象如图所示,则下列结论正确的是( )[-12,4]组卷:581引用:8难度:0.7 -
4.1614年纳皮尔在研究天文学的过程中为了简化计算而发明对数;1637年笛卡尔开始使用指数运算;1770年,欧拉发现了指数与对数的互逆关系,指出:对数源于指数,对数的发明先于指数,成为历史上的珍闻.若
,lg2=0.3010,则x的值约为( )2x=52组卷:1301引用:13难度:0.8 -
5.“|m|<1”是“方程x2-mx+1=0无实数解”的( )
组卷:284引用:7难度:0.7 -
6.函数
的图象大致为( )f(x)=xcosxe|x|组卷:257引用:9难度:0.7 -
7.已知曲线y=lnx的切线过原点,则此切线的斜率为( )
组卷:5140引用:17难度:0.7
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数f(x)=loga(3-x),g(x)=loga(3+x),其中a>0,a≠1.
(1)判断函数h(x)=f(x)-g(x)的奇偶性,并说明理由;
(2)若∀x∈(,12),都有2f(x)<g(ax)成立,求a的取值范围.54组卷:212引用:3难度:0.4 -
22.已知函数f(x)=cosx+axsinx.
(1)若a=1,求曲线y=f(x)在点(π,f(π))处的切线方程;
(2)若x=0是f(x)的极大值点,求a的取值范围.组卷:50引用:2难度:0.3


