2022-2023学年黑龙江省七台河市勃利高级中学高一（下）期末数学试卷

一、选择题：（本大题共8小题，每题5分，共计40分，在每题给出的四个选项中，只有一个是正确的）

• 1．设i是虚数单位，若复数

  z

  =

  i

  1

  +

  i

  ，则z的共轭复数的虚部为（　　）

  A．- 1 2

  B． - 1 2 i

  C． 1 2 i

  D． 1 2
  组卷：12引用：1难度：0.8

  解析

• 2．已知单位向量

  a

  ，

  b

  满足（2

  a

  +

  b

  ）⊥

  b

  ，则

  a

  与

  b

  的夹角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：762引用：6难度：0.8

  解析

• 3．已知△ABC的三边分别是a,b,c,设向量

  m

  =

  （

  sin

  B

  -

  sin

  A

  ，

  3

  a

  +

  c

  ）

  ，

  n

  =

  （

  sin

  C

  ，

  a

  +

  b

  ）

  ，且

  m

  ∥

  n

  ，则B的大小是（　　）

  A． π 6

  B． 5 π 6

  C． π 3

  D． 2 π 3
  组卷：778引用：9难度：0.5

  解析

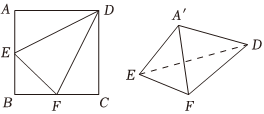• 4．如图，边长为2的正方形ABCD中，点E、F分别是AB、BC的中点，将△ADE、△EBF、△FCD，分别沿DE、EF、FD折起，使得A、B、C三点重合于点A'，若四面体A'EFD的四个顶点在同一个球面上，则该球的表面积为（　　）

  A．5π

  B．6π

  C．8π

  D．10π
  组卷：36引用：2难度：0.5

  解析

• 5．在下列条件中，可判断平面α与β平行的是（　　）

  A．α⊥γ，且β⊥γ

  B．m,n是两条异面直线，且m∥β，n∥β，m∥α，n∥α

  C．m,n是α内的两条直线，且m∥β，n∥β

  D．α内存在不共线的三点到β的距离相等
  组卷：131引用：5难度：0.9

  解析

• 6．为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10m到位置D，测得∠BDC=45°，则塔AB的高是（　　）

  A．10 m

  B．10 2  m

  C．10 3  m

  D．10 6  m
  组卷：136引用：9难度：0.9

  解析

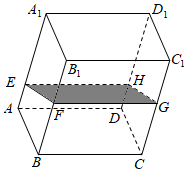• 7．如图，在透明塑料制成的长方体ABCD-A₁B₁C₁D₁容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：
  ①有水的部分始终呈棱柱形；
  ②水面EFGH所在的四边形面积为定值；
  ③棱A₁D₁始终与水面所在的平面平行；
  ④当点E在棱AA₁时，AE+BF是定值．
  其中正确说法的是（　　）

  A．①②④

  B．①③④

  C．①②③

  D．②③④
  组卷：73引用：2难度：0.5

  解析

四、解答题：（本大题共6小题，共计70分。解答应写出文字说明、证明过程或演算步骤）

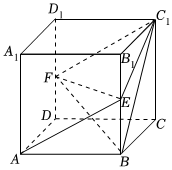• 21．如图所示，正方体ABCD-A₁B₁C₁D₁中，点E在棱BB₁上运动，F为DD₁的中点
  （1）若E为BB₁中点，求证：AE∥平面BC₁F；
  （2）若

  BE

  B

  B

  1

  =λ，求当λ为何值时，二面角B-C₁F-E的平面角的余弦值为

  4

  21

  21

  ．
  组卷：68引用：2难度：0.5

  解析

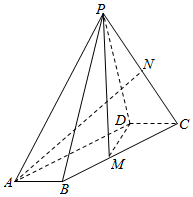• 22．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=120°，AB=1，BC=4，

  PA

  =

  15

  ，M，N分别为BC，PC的中点，PD⊥DC，PM⊥MD．
  （1）证明：DC⊥PM；
  （2）求直线AN与平面PCM所成角的正弦值．
  组卷：381引用：5难度：0.4

  解析