2022-2023学年广东省东莞实验中学高三（上）月考数学试卷（一）

一、选择题：（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若集

  A

  =

  {

  x

  |

  x

  ≤

  2

  }

  ，

  B

  =

  {

  x

  |

  3

  x

  -

  2

  ≥

  1

  }

  ，则A∩B=（　　）

  A．{x|0≤x≤4}

  B．{x|1≤x≤4}

  C．{x|1≤x≤3}

  D．{x|2≤x≤3}
  组卷：57引用：2难度：0.8

  解析

• 2．已知复数

  z

  =

  2

  1

  +

  i

  （i为虚数单位），则复数z的共轭复数

  z

  在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：34引用：3难度：0.7

  解析

• 3．已知直线l,m与平面α，其中m⊂α，则“l⊥m”是“l⊥α”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：121引用：7难度：0.9

  解析

• 4．某日，甲、乙、丙三个单位被系统随机预约到A，B，C三家医院接种疫苗且每个单位只能被随机预约到一家医院，每家医院每日至多接待两个单位．已知A医院接种的是只需要打一针的腺病毒载体疫苗，B医院接种的是需要打两针的灭活疫苗，C医院接种的是需要打三针的重组蛋白疫苗，则甲单位不接种需要打三针的重组蛋白疫苗的预约方案种数为（　　）

  A．27

  B．24

  C．18

  D．16
  组卷：10引用：2难度：0.6

  解析

• 5．已知m,n∈R，且m+

  n

  2

  =1，则9^m+3ⁿ的最小值为（　　）

  A．4

  B．6

  C．8

  D．9
  组卷：623引用：5难度：0.8

  解析

• 6．四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是边长为1的菱形，侧棱长为2，且∠C₁CB=∠C₁CD=∠BCD=60°，则线段A₁C的长度是（　　）

  A． 6

  B． 34 2

  C．3

  D． 11
  组卷：693引用：6难度：0.7

  解析

• 7．若0＜x₁＜x₂≤a都有x₂lnx₁-x₁lnx₂＜x₁-x₂成立，则a的最大值为（　　）

  A． 1 2

  B．1

  C．e

  D．2e
  组卷：71引用：4难度：0.7

  解析

四、解答题：本大题共6小题，共70分．其中第17题10分，其余题目12分．解答应写出文字说明，证明过程或演算步骤．

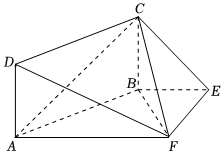• 21．如图，四边形ABCD是矩形，四边形ABEF是梯形，BE∥AF，BE⊥EF，∠BAF=30°，平面ABCD与平面ABEF互相垂直，BF=2，AF=4．
  （1）求证：BF⊥AC．
  （2）若二面角C-AF-B为

  π

  6

  ，求多面体ABCDEF的体积．
  组卷：34引用：4难度：0.6

  解析

• 22．已知函数f（x）=x+

  e

  x

  x

  ，g（x）=x+alnx（a∈R）．
  （1）讨论函数g（x）的单调性；
  （2）证明：当a∈（0，

  e

  2

  2

  ]时，f（x）＞g（x）在（0，+∞）上恒成立．
  组卷：27引用：4难度：0.3

  解析