2022-2023学年天津第二南开中学八年级（下）期末数学试卷

一.单选题。（本大题共12小题，每小题3分，共36分。）

• 1．若

  x

  +

  2023

  有意义，则x的取值范围是（　　）

  A．x≥2023

  B．x≥-2023

  C．x＞2023

  D．x＞-2023
  组卷：187引用：6难度：0.8

  解析

• 2．下列计算正确的是（　　）

  A． （ - 2 ） × （ - 3 ） = - 2 × - 3	B． 3 - 2 = 1
  C． （ - 2 ） 2 = 2	D． （ 3 2 ） 2 = 6
  组卷：224引用：3难度：0.7

  解析

• 3．如图，在平面直角坐标系xOy中，平行四边形ABCD的顶点A，B，C的坐标分别是（-2，0），（3，0），（0，6），则顶点D的坐标是（　　）

  A．（4，5）

  B．（-4，5）

  C．（5，6）

  D．（-5，6）
  组卷：334引用：3难度：0.6

  解析

• 4．已知点A（-2，m），B（3，n）在一次函数y=2x+1的图象上，则m与n的大小关系是（　　）

  A．m＞n

  B．m=n

  C．m＜n

  D．无法确定
  组卷：1303引用：13难度：0.6

  解析

• 5．如图，数轴上点A表示的数为-1，Rt△ABC的直角边AB落在数轴上，且AB长为3个单位长度，BC长为1个单位长度，若以点A为圆心，以斜边AC长为半径画弧交数轴于点D，则点D表示的数为（　　）

  A． 10

  B． 5 - 1

  C． 5

  D． 10 - 1
  组卷：1021引用：7难度：0.6

  解析

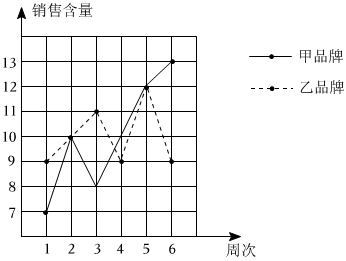• 6．某家电销售商店周销售甲、乙两种品牌冰箱的数量如图所示（单位：台），如果两种品牌冰箱周销售量的方差为

  S

  2

  1

  ，

  S

  2

  2

  ，则

  S

  2

  1

  与

  S

  2

  2

  的大小关系是（　　）

  A． S 2 1 ＞ S 2 2

  B． S 2 1 ＜ S 2 2

  C． S 2 1 = S 2 2

  D．不能确定
  组卷：137引用：2难度：0.7

  解析

• 7．小玲的爸爸在制作平行四边形框架时，采用了一种方法：如图所示，将两根木条AC，BD的中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（　　）

  A．对角线互相平分的四边形是平行四边形

  B．两组对角分别相等的四边形是平行四边形

  C．两组对边分别相等的四边形是平行四边形

  D．两组对边分别平行的四边形是平行四边形
  组卷：893引用：8难度：0.7

  解析

• 8．已知在四边形ABCD中，对角线AC与BD相等，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是（　　）

  A．平行四边形

  B．矩形

  C．菱形

  D．正方形
  组卷：141引用：2难度：0.6

  解析

三.解答题。（本大题共7小题，共66分.解答应写出文字说明、演算步理或推理过程）

• 24．如图，正方形ABCD中，AB=4，点E是对角线AC上的一点，连接DE，过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩形DEFG，连接AG．
  （1）求证：矩形DEFG是正方形；
  （2）求AG+AE的值；
  （3）若F恰为AB的中点，连接DF，求点E到DF的距离．
  组卷：1134引用：5难度：0.4

  解析

• 25．如图1，一次函数y=

  3

  4

  x-6的图象与坐标轴交于点A，B，BC平分∠OBA交x轴于点C，CD⊥AB，垂足为D．
  （1）求点A，B的坐标；
  （2）求CD所在直线的解析式；
  （3）如图2，点E是线段OB上的一点，点F是线段BC上的一点，求EF+OF的最小值．
  
  组卷：1627引用：4难度：0.2

  解析