2022-2023学年河北省唐山市路南区八年级（上）期中数学试卷

一、选择题（本大题共12个小题。每小题2分，共24分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．观察下列图形，其中是三角形的是（　　）

  A．

  B．

  C．

  D．
  组卷：785引用：10难度：0.9

  解析

• 2．某三角形的三边长分别为3，6，x,则x可能是（　　）

  A．3

  B．9

  C．6

  D．10
  组卷：411引用：10难度：0.8

  解析

• 3．下列计算正确的是（　　）

  A．a6÷a2=a4

  B．（a5）2=a7

  C．（ab2）3=ab6

  D．a2•a3=a6
  组卷：77引用：3难度：0.7

  解析

• 4．一个多边形的内角和为α，外角和为β，则α=2β的多边形的是（　　）

  A．

  B．

  C．

  D．
  组卷：213引用：8难度：0.7

  解析

• 5．计算

  （

  a

  2

  +

  a

  2

  +

  ⋯

  +

  a

  2

  5

  个

  a

  2

  ）

  3

  的结果是（　　）

  A．125a6

  B．15a5

  C．a30

  D．a13
  组卷：711引用：4难度：0.7

  解析

• 6．已知（x+2）²=0，则x³的值等于（　　）

  A．8

  B．2

  C．-3

  D．-8
  组卷：46引用：2难度：0.5

  解析

• 7．长方形面积是3a²-3ab+6a,一边长为3a,则它的另一条边长为（　　）

  A．2a-b+2

  B．a-b+2

  C．3a-b+2

  D．4a-b+2
  组卷：256引用：3难度：0.9

  解析

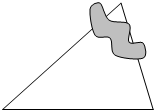• 8．如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画出了一个与书上完全一样的三角形，那么小明画图的依据是（　　）

  A．SSS

  B．SAS

  C．AAS

  D．ASA
  组卷：4630引用：78难度：0.8

  解析

三、解答题（本大题共7个小题：共58分）

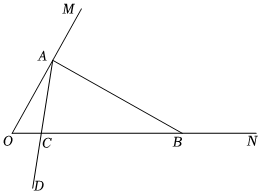• 24．在一个钝角三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“智慧三角形”．如图，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C．
  （1）∠ABO的度数为

  °，△AOB

  （填“是”或“不是”）“智慧三角形”；
  （2）若∠OAC=20°，求证：△AOC为“智慧三角形”；
  （3）当△ABC为“智慧三角形”时，求∠OAC的度数．（直接写出答案）
  组卷：216引用：3难度：0.5

  解析

• 25．问题背景：
  
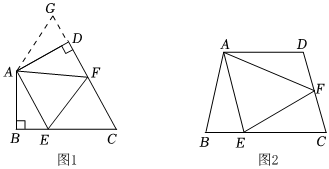
  （1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE、EF、FD之间的数量关系，嘉琪同学探究此问题的方法是：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是

  ．
  （2）探索延伸：①如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF=

  1

  2

  ∠BAD，上述结论是否仍然成立，并说明理由．
  ②如图2，若五边形ABEFD的面积为30，BE=4，DF=6，直接写出A点到EF的距离．
  组卷：301引用：3难度：0.2

  解析