2023-2024学年广西南宁三十六中高二（上）月考数学试卷（10月份）

一、单项选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若A，B，C，D为空间任意四个点，则

  AB

  +

  DA

  -

  DC

  =（　　）

  A． CB

  B． BC

  C． BD

  D． AC
  组卷：279引用：2难度：0.8

  解析

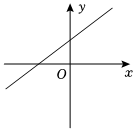• 2．已知直线l：

  x

  A

  +

  y

  B

  =C，则以下四个情况中，可以使l的图象如图所示的为（　　）

  A．A＞0，B＜0，C＞0	B．A＜0，B＜0，C＞0
  C．A＜0，B＜0，C＜0	D．A＞0，B＜0，C＜0
  组卷：89引用：5难度：0.7

  解析

• 3．

  a

  =

  （

  -

  1

  ，

  2

  ，-

  3

  ）

  ，

  b

  =

  （

  2

  ，

  x

  ,

  6

  ）

  ，若

  a

  ∥

  b

  ，则x=（　　）

  A．0

  B．-4

  C．4

  D．2
  组卷：80引用：5难度：0.8

  解析

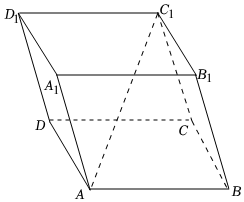• 4．如图所示，平行六面体ABCD-A₁B₁C₁D₁中，AB=AD=AA₁=1，∠BAD=∠BAA₁=120°，若线段

  A

  C

  1

  =

  2

  ，则∠DAA₁=（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：72引用：3难度：0.7

  解析

• 5．直线xcosα+y+4=0的倾斜角的取值范围（　　）

  A．[0，π）	B． [ 0 ， π 4 ] ∪ （ π 2 ， π ）
  C． [ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）	D． [ 0 ， π 4 ]
  组卷：150引用：6难度：0.7

  解析

• 6．已知向量

  a

  =

  （

  2

  3

  ，

  0

  ，

  2

  ）

  ，向量

  b

  =

  （

  1

  2

  ，

  0

  ，

  3

  2

  ）

  ，则向量

  a

  在向量

  b

  上的投影向量为（　　）

  A． （ 3 ， 0 ， 3 ）

  B． （ - 3 ， 0 ， 1 ）

  C． （ 1 ， 0 ， 3 ）

  D． （ 1 4 ， 0 ， 3 4 ）
  组卷：285引用：14难度：0.9

  解析

• 7．从P点发出的光线l经过直线x-y-2=0反射，若反射光线恰好通过点Q（5，1），且点P的坐标为（3，-2），则光线l所在的直线方程是（　　）

  A．x=3

  B．y=1

  C．x-2y-7=0

  D．x+2y+1=0
  组卷：54引用：1难度：0.7

  解析

四、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤）.

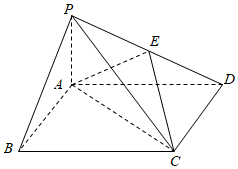• 21．在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，E为PD的中点．
  （Ⅰ）证明：PB∥平面AEC；
  （Ⅱ）若PA=2，AD=4，求直线CE与平面ABCD所成的角正切值．
  组卷：155引用：2难度：0.7

  解析

• 22．请从①cos2C+cosC=0；②sin²A+sin²B-sin²C-sinAsinB=0；③ccosB+（b-2a）cosC=0这三个条件中任选一个，补充在下面问题中，并加以解答（如未作出选择，则按照选择①评分．选择的编号请填写到答题卡对应位置上）．
  （1）求角C的大小；
  （2）若c=1，D为△ABC的外接圆上的点，

  BA

  •

  BD

  =

  BA

  2

  ，求四边形ABCD面积的最大值．
  组卷：59引用：3难度：0.6

  解析