2023-2024学年广东省广州市增城一中高三（上）月考数学试卷（9月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知全集U=R，集合A={x|x＞1}，B={x|-2≤x＜2}，则如图中阴影部分表示的集合为（　　）

  A．{x|x≥-2}

  B．{x|x＜-2}

  C．{x|1＜x＜2}

  D．{x|x≤1}
  组卷：63引用：5难度：0.7

  解析

• 2．下列函数中，在区间（0，+∞）上单调递增的是（　　）

  A．f（x）=-lnx

  B． f （ x ） = 1 2 x

  C． f （ x ） = - 1 x

  D．f（x）=3|x-1|
  组卷：1545引用：22难度：0.7

  解析

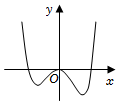• 3．已知函数f（x）的导函数的图象如图所示，则f（x）的极值点的个数为（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：215引用：8难度：0.7

  解析

• 4．已知

  sinθ

  =

  3

  5

  ，则

  sin

  （

  -

  θ

  ）

  cos

  （

  π

  -

  θ

  ）

  sin

  （

  π

  2

  -

  θ

  ）

  =（　　）

  A． - 4 5

  B． 4 5

  C． - 3 5

  D． 3 5
  组卷：425引用：1难度：0.5

  解析

• 5．科学家康斯坦丁•齐奥尔科夫斯基在1903年提出单级火箭在不考虑空气阻力和地球引力的理想情况下的最大v满足公式：

  v

  =

  v

  0

  ln

  m

  1

  +

  m

  2

  m

  1

  ，其中m₁，m₂分别为火箭结构质量和推进剂的质量，v₀是发动机的喷气速度．已知某实验用的单级火箭模型结构质量为akg,若添加推进剂3akg,火箭的最大速度为2.8km/s,若添加推进剂5akg,则火箭的最大速度约为（　　）（参考数据：ln2≈0.7，ln3≈1.1）

  A．4.7km/s

  B．4.2km/s

  C．3.6km/s

  D．3.1km/s
  组卷：195引用：6难度：0.6

  解析

• 6．函数

  f

  （

  x

  ）

  =

  sinx

  e

  |

  x

  |

  在[-π，π]上大致的图象为（　　）

  A．	B．
  C．	D．
  组卷：89引用：5难度：0.6

  解析

• 7．设函数f（x）=

  lo g 2 （ 6 - x ） ， x ＜ 1

  2 x - 1 ， x ≥ 1

  ，则f（-2）+f（log₂6）=（　　）

  A．2

  B．6

  C．8

  D．10
  组卷：209引用：4难度：0.8

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．小王大学毕业后，决定利用所学专业进行自主创业．经过市场调查，生产某小型电子产品需投入年固定成本为3万元，每生产x万件，需另投入流动成本为W（x）万元，在年产量不足8万件时，

  W

  （

  x

  ）

  =

  1

  3

  x

  2

  +

  x

  （万元）．在年产量不小于8万件时，

  W

  （

  x

  ）

  =

  6

  x

  +

  100

  x

  -

  38

  （万元）．每件产品售价为5元．通过市场分析，小王生产的商品能当年全部售完．
  （Ⅰ）写出年利润L（x）（万元）关于年产量x（万件）的函数解析式；
  （注：年利润=年销售收入-固定成本-流动成本）
  （Ⅱ）年产量为多少万件时，小王在这一商品的生产中所获利润最大？最大利润是多少？
  组卷：226引用：29难度：0.5

  解析

• 22．已知

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  4

  x

  +

  alnx

  ．
  （1）若函数f（x）在区间（0，+∞）上单调递增，求实数a的取值范围；
  （2）若函数f（x）有两个极值点x₁，x₂，证明：f（x₁）+f（x₂）＞-10+lna.
  组卷：49引用：4难度：0.2

  解析