2023年山东省枣庄市薛城区中考数学二模试卷
发布：2024/5/30 8:0:9
一、选择题：下面每小题给出的四个选项中，只有一项是正确的，请把正确选项选出来.每小题3分，共30分.
-
1．-
的相反数是（ ）13组卷：2045引用：503难度：0.9 -
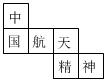2．为了发扬“中国航天精神”，每年的4月24日设立为“中国航天日”．正方体的每个面上都有一个汉字，如图是它的一种平面展开图，那么在原正方体中，与“国”字所在面相对的面上的汉字是（ ）组卷：330引用：5难度：0.7 -
3．下列图案中，任意选取一个图案，既是中心对称图形也是轴对称图形的为（ ）
组卷：143引用：6难度：0.9 -
4．代数式
有意义时，直线y=kx+k一定不经过（ ）k-1组卷：665引用：2难度：0.8 -
5．一组数据x1，x2，…，x7的方差是S2=
，则该组数据的和为（ ）17[（x1-3）2+（x2-3）2+⃯+（x7-3）2]组卷：268引用：5难度：0.8 -
6．根据研究，运动员未运动时，体内血乳酸浓度通常在40mg/L以下；运动员进行高强度运动后，如果血乳酸浓度降到50mg/L以下，运动员就基本消除了疲劳．体育科研工作者根据实验数据，绘制了一幅图象，如图和表所示，它反映了运动员进行高强度运动后，体内血乳酸浓度随时间变化而变化的函数关系．下列叙述正确的是（ ）图中曲线①表示采用慢跑活动方式放松时血乳酸浓度的变化情况；
曲线②表示采用静坐方式休息时血乳酸浓度的变化情况组卷：131引用：3难度：0.8 -
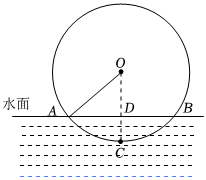7．唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船的轮子被水面截得的弦AB长8m,轮子的吃水深度CD为2m,则该桨轮船的轮子直径为（ ）组卷：901引用：6难度：0.5 -
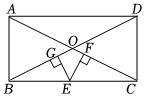8．出入相补原理是我国古代数学的重要成就之一，最早是由三国时期数学家刘徽创建，“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和”是该原理的重要内容之一，如图，在矩形ABCD中，AB=1，AD=2，AC，BD交于点O，E为边BC上一点，EF⊥AC，EG⊥BD，垂足分别为点F，G，则EF+EG等于（ ）组卷：554引用：4难度：0.6
三、解答题（本题共8道大题，共72分）
-
23．已知△ABC≌△DEC，AB=AC，AB＞BC．
（1）如图1，CB平分∠ACD，求证：四边形ABDC是菱形；
（2）如图2，将（1）中的△CDE绕点C逆时针旋转（旋转角小于∠BAC），BC，DE的延长线相交于点F，用等式表示∠ACE与∠EFC之间的数量关系，并证明；
（3）如图3，将（1）中的△CDE绕点C顺时针旋转（旋转角小于∠ABC），若∠BAD=∠BCD，求∠ADB的度数．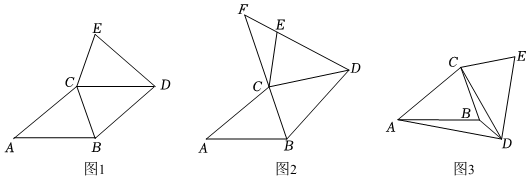
组卷：3131引用：8难度：0.3 -
24．如图所示，将抛物线y=
x2沿x轴向右平移2个单位长度，再向下平移1个单位长度，得到新的抛物线．12
（1）直接写出新抛物线的解析式为；
（2）设新抛物线交x轴于A、B两点，交y轴于C，顶点为D，作CE⊥CD交抛物线于E，如图所示，探究如下问题：
①求点E的坐标；
②若一次函数y=kx+1的图象与抛物线存在唯一交点且交对称轴交于点F，连接DE，猜测直线DE与对称轴的夹角和一次函数y=kx+1的图象与对称轴的夹角之间的大小关系，并证明．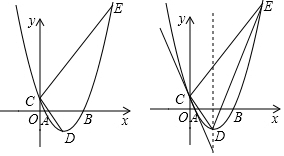
组卷：243引用：4难度：0.5
