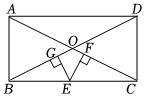
出入相补原理是我国古代数学的重要成就之一，最早是由三国时期数学家刘徽创建，“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和”是该原理的重要内容之一，如图，在矩形ABCD中，AB=1，AD=2，AC，BD交于点O，E为边BC上一点，EF⊥AC，EG⊥BD，垂足分别为点F，G，则EF+EG等于（ ）
【考点】矩形的性质．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/30 8:0:9组卷：554引用：4难度：0.6
相似题
-
1．如图，平行四边形ABCD，对角线AC、BD相交于点O，AC=20cm,BD=12cm,E、F是对角线AC上的两个动点，点E从点A开始向点C匀速运动，点F从点C开始向点A匀速运动，点E和点F同时出发，且运动速度均为2cm/s.
（1）求证：当E、F运动过程中不与点O重合时，四边形BEDF是平行四边形；
（2）若四边形BEDF为矩形，求动点E、F运动时间．发布：2025/5/23 10:30:1组卷：314引用：3难度：0.6 -
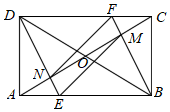2．如图，矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC交CD于点F，交AC于点M，过点D作DE∥BF交AB于点E，交AC于点N，连接FN，EM．则下列结论：①DN=BM；②EM∥FN；③DF=NF；④当AO=AD时，四边形DEBF是菱形．其中正确的结论是 ．发布：2025/5/23 9:0:2组卷：215引用：2难度：0.3 -
3．如图，在矩形ABCD中，M是BC上的动点，E，F分别是AM，MC的中点，则EF的长随着M点的运动（ ）发布：2025/5/23 9:30:1组卷：485引用：2难度：0.7
