2022-2023学年四川省成都市郫都区高一(下)期末数学试卷
发布:2024/6/2 8:0:8
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)
-
1.复数
的虚部为( )1+i1-i组卷:140引用:8难度:0.9 -
2.若两个非零向量
,a满足b,则( )|a+b|=|a-b|组卷:198引用:2难度:0.7 -
3.在△ABC中,角A,B,C的对边分别为a,b,c.若sinA:sinB:sinC=4:5:6,则cosA=( )
组卷:210引用:4难度:0.7 -
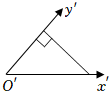 4.如图,已知△ABC通过斜二测画法得到的直观图是面积为2的等腰直角三角形,则△ABC为( )组卷:111引用:3难度:0.8
4.如图,已知△ABC通过斜二测画法得到的直观图是面积为2的等腰直角三角形,则△ABC为( )组卷:111引用:3难度:0.8 -
 5.龙洗,是我国著名的文物之一,因盆内有龙线,故称龙洗,为古代皇宫盥洗用具,其盆体可以近似看作一个圆台.现有一龙洗盆高18cm,盆口直径36cm,盆底直径18cm.现往盆内注水,当水深为6cm时,则盆内水的体积为( )组卷:113引用:7难度:0.5
5.龙洗,是我国著名的文物之一,因盆内有龙线,故称龙洗,为古代皇宫盥洗用具,其盆体可以近似看作一个圆台.现有一龙洗盆高18cm,盆口直径36cm,盆底直径18cm.现往盆内注水,当水深为6cm时,则盆内水的体积为( )组卷:113引用:7难度:0.5 -
6.已知a,b是两条不同的直线,且a∥平面α,则“b⊥α”是“a⊥b”的( )
组卷:131引用:3难度:0.8 -
7.已知tanα+tanβ=-6,tan(α+β)=-1,则
=( )sin(α+β)cos(α-β)组卷:122引用:1难度:0.7
四、解答题(本大题共6小题共70分,解答应写出文字说明,证明过程或演算步骤)
-
21.在△ABC中,角A,B,C的对边分别为
.a,b,c,3bsinA=a(1+cosB)
(1)求B;
(2)若,点M在边AC上,连接BM并延长至点D,且a=1,b=3.求△ACD面积的最大值及此时点M的位置.∠ADC=2π3组卷:226引用:2难度:0.5 -
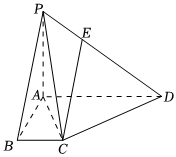 22.如图,四棱锥P-ABCD的底面为直角梯形,BC∥AD,AD=4BC=4,AP=2,PA⊥底面ABCD,平面PAC⊥平面PCD,点E在棱PD上,且PD=4PE.
22.如图,四棱锥P-ABCD的底面为直角梯形,BC∥AD,AD=4BC=4,AP=2,PA⊥底面ABCD,平面PAC⊥平面PCD,点E在棱PD上,且PD=4PE.
(1)证明:CE∥平面PAB;
(2)求二面角P-CD-A的正弦值.组卷:132引用:1难度:0.6


