2023-2024学年北京市朝阳区陈经纶中学高三（上）诊断数学试卷（9月份）

一、选择题（本题共10题，每小题4分，满分40分）

• 1．设全集为R，若集合A={x|x²＜4}，B={x|log₂x＞0}，则A∩（∁_RB）=（　　）

  A．{x|1＜x＜2}

  B．{x|-2＜x≤1}

  C．{x|1≤x＜2}

  D．{x|-2＜x＜1}
  组卷：88引用：4难度：0.8

  解析

• 2．设复数z满足

  z

  1

  -

  i

  =

  1

  +

  2

  i

  ，则它的共轭复数

  z

  的虚部为（　　）

  A．-1

  B．1

  C．-i

  D．i
  组卷：48引用：2难度：0.7

  解析

• 3．下列函数中，是奇函数且在定义域内单调递减的是（　　）

  A．f（x）=sinx	B．f（x）=2|x|
  C．f（x）= 2 x	D．f（x）= 1 2 （ e - x - e x ）
  组卷：27引用：5难度：0.7

  解析

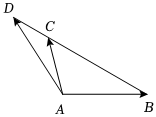• 4．如图所示，点C在线段BD上，且BC=3CD，则

  AD

  =（　　）

  A． 3 AC - 2 AB

  B． 4 AC - 3 AB

  C． 4 3 AC - 1 3 AB

  D． 1 3 AC - 2 3 AB
  组卷：124引用：6难度：0.7

  解析

• 5．已知直线m,直线n和平面α，则下列四个命题中正确的是（　　）

  A．若m∥α，n⊂α，则m∥n	B．若m∥α，n∥α，则m∥n
  C．若m⊥α，n∥α，则m⊥n	D．若m⊥n,n∥α，则m⊥α
  组卷：625引用：6难度：0.7

  解析

• 6．若a,b为实数，且0＜ab＜1，则以下结论中正确的是（　　）

  A． a ＜ 1 b

  B．a＞0，b＞0

  C．0＜a3b2＜1

  D． - 1 ab ＜ - 1
  组卷：119引用：4难度：0.7

  解析

• 7．函数f（x）=cos2x+6cos（

  π

  2

  -x）（x∈[0，

  π

  2

  ]）的最大值为（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：462引用：4难度：0.7

  解析

三、解答题（本题共6题，满分85分）

• 20．已知函数f（x）=e^x-ax+cosx-2．
  （Ⅰ）求曲线y=f（x）在点（0，f（0））处的切线方程；
  （Ⅱ）若f（x）在（0，+∞）上单调递增，求实数a的取值范围；
  （Ⅲ）当a＞1时，判断f（x）在（0，+∞）零点的个数，并说明理由．
  组卷：172引用：6难度：0.2

  解析

• 21．设数列{a_n}满足：a₁=1，

  a

  n

  =

  a

  n

  -

  1

  +

  a

  [

  n

  2

  ]

  ，n=2，3，…，其中[x]表示不超过实数x的最大整数．若a_n被正整数p除所得的余数为k,则记a_n=k（modp），若数列中不同的两项a_i，a_j被p除所得余数相同，则记a_i=a_j（modp）．
  （Ⅰ）直接写出a₂，a₃，a₄，a₅；
  （Ⅱ）若a_n≡0（mod7），证明：a_2n+1≡a_2n≡a_2n-1（mod7）；
  （Ⅲ）证明：数列{a_n}有无穷多项是7的倍数．
  组卷：30引用：1难度：0.5

  解析