2022-2023学年福建省漳州外国语学校八年级(下)月考数学试卷(5月份)
发布:2024/7/11 8:0:9
一、单选题(本大题共10小题,共40分)
-
1.下列各式中:
,x+y2,-3ba,1x+y,分式的个数为( )3+yπ组卷:121引用:3难度:0.6 -
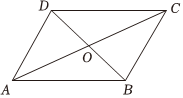 2.如图,四边形ABCD的对角线交于点O,下列不能判定其为平行四边形的是( )组卷:391引用:7难度:0.6
2.如图,四边形ABCD的对角线交于点O,下列不能判定其为平行四边形的是( )组卷:391引用:7难度:0.6 -
3.若一个多边形的内角和是540°,则该多边形的边数为( )
组卷:2076引用:73难度:0.9 -
4.下列分式是最简分式的是( )
组卷:334引用:7难度:0.5 -
5.如图是嘉琪进行分式计算的过程,下列判断不正确的是( )
=2xx2-1-1x+1第一步2x(x+1)(x-1)-1x+1
=第二步2x(x+1)(x-1)-x-1(x+1)(x-1)
=2x-(x-1)第三步
=x+1第四步组卷:206引用:4难度:0.7 -
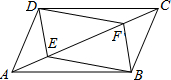 6.如图,点E、F是平行四边形ABCD对角线上两点,在条件:①DE=BF;②∠ADE=∠CBF;③AF=CE;④∠AFB=∠CED中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )组卷:920引用:6难度:0.5
6.如图,点E、F是平行四边形ABCD对角线上两点,在条件:①DE=BF;②∠ADE=∠CBF;③AF=CE;④∠AFB=∠CED中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )组卷:920引用:6难度:0.5 -
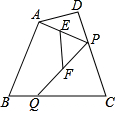 7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度( )组卷:4883引用:13难度:0.7
7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度( )组卷:4883引用:13难度:0.7 -
8.下列说法错误的是( )
组卷:888引用:4难度:0.5
三、解答题(本大题共9小题,共86分)
-
24.我们定义:形如
(m,n不为零),且两个解分别为x1=m,x2=n的方程称为“十字分式方程”.x+mnx=m+n
例如为十字分式方程,可化为x+6x=5,∴x1=2,x2=3.x+2×3x=2+3
再如为十字分式方程,可化为x+7x=-8.∴x1=-1,x2=-7.x+(-1)×(-7)x=(-1)+(-7)
应用上面的结论解答下列问题:
(1)若为十字分式方程,则x1=,x2=.x+12x=-7
(2)若十字分式方程的两个解分别为x1=a,x2=b,求x-6x=-5的值.ba+ab+1
(3)若关于x的十字分式方程的两个解分别为x1,x2(k>2,x1>x2),求x-2023k-2022k2x-1=2023k-2022的值.x1+4044x2组卷:682引用:6难度:0.7 -
25.如图,在平面直角坐标系中,直线AB交x轴于点A(-2,0),交y轴于点B(0,4),直线y=kx+b经过点B且交x轴正半轴于点C,已知AC=5.
(1)点C的坐标是( ,),直线BC的表达式是 ;
(2)如图1,点E为线段AB中点,点D为y轴上一动点,以DE为直角边作等腰直角三角形△EDF,且DE=DF,当点F落在直线BC上时,求点D的坐标;
(3)如图2,若G为线段BC上一点,且满足S△ABG=S△ABO,点M为直线AG上一动点,在x轴上是否存在点N,使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,说明理由.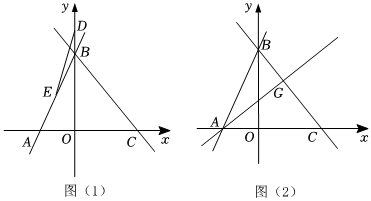 组卷:181引用:1难度:0.3
组卷:181引用:1难度:0.3


