当前位置：试卷中心 > 试卷详情

2023-2024学年山东省临沂市高三（上）期中数学试卷

发布：2024/10/24 14:0:2

1．设集合A={x|3^x＞1}，B={x|x²-3x＜0}，则A∩B=（　　）
A．[0，3） B．[1，3） C．（0，3） D．（1，3）
组卷：19引用：3难度：0.9
解析
2．若复数z=i（i+1），则
z
的虚部为（　　）
A．-1 B．-i C．1 D．i
组卷：20引用：2难度：0.8
解析
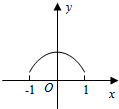3．已知函数y=f（x）的图象是下列四个图象之一，且其导函数y=f′（x）的图象如图所示，则该函数的图象是（　　）
A． B． C． D．
组卷：1920引用：99难度：0.9
解析
4．若a＞0，b＞0，则“a+b＜4”是“ab＜4”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：265引用：4难度：0.8
解析
5．已知角α的顶点与原点重合，始边与x轴正半轴重合，终边经过点（1，-2），则tan2α=（　　）
A．
-
3
4
B．
3
4
C．
-
4
3
D．
4
3
组卷：404引用：7难度：0.8
解析
6．已知公比不为1的正项等比数列{a_n}满足
a
2
3
=a_ma_n（m,n∈N^*），则
4
m
+
1
n
的最小值为（　　）
A．6 B．2 C．
3
2
D．
1
2
组卷：55引用：2难度：0.5
解析
7．已知
a
=
cos
π
5
，
b
=
sin
π
4
，c=log₃2，则（　　）
A．b＜a＜c B．b＜c＜a C．c＜a＜b D．c＜b＜a
组卷：50引用：3难度：0.7
解析

21．已知等差数列{a_n}的前n项和为S_n，a₁=2，S₄=14，数列{b_n}满足b₁=4，b_n+1=3b_n-2．
（1）求{b_n}的通项公式；
（2）设数列{c_n}满足：
c
n
=
a
n
+
1
a
2
n
•
a
2
n
+
2
，
n
为奇数
1
b
n
，
n
为偶数
，若{c_n}的前n项和为T_n，证明：
T
2
n
＜
3
16
．
组卷：180引用：6难度：0.3
解析
22．已知函数f（x）=x²-ax+2lnx,a∈R．
（1）讨论f（x）的单调性；
（2）已知f（x）有两个极值点x₁，x₂，且x₁＜x₂，证明：2f（x₁）-f（x₂）≥-1-3ln2．
组卷：185引用：3难度：0.2
解析

A．充分不必要条件	B．必要不充分条件
C．充分必要条件	D．既不充分也不必要条件

a n + 1 a 2 n • a 2 n + 2 ，	n 为奇数
1 b n ，	n 为偶数

1．设集合A={x|3x＞1}，B={x|x2-3x＜0}，则A∩B=（ ）