2023-2024学年重庆市荣昌中学高二（上）第一次月考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.

• 1．若复数z=i（2+i），则|z|=（　　）

  A．1

  B． 2

  C．5

  D． 5
  组卷：147引用：5难度：0.8

  解析

• 2．已知空间向量

  m

  =（3，1，3），

  n

  =（-1，λ，-1），且

  m

  ∥

  n

  ，则实数λ=（　　）

  A．- 1 3

  B．-3

  C． 1 3

  D．6
  组卷：1174引用：11难度：0.8

  解析

• 3．设l是一条直线，α，β是两个不同的平面，下列命题正确的是（　　）

  A．若l∥α，l∥β，则α∥β	B．若α⊥β，l∥α，则l⊥β
  C．若l∥α，l⊥β，则α⊥β	D．若α⊥β，l⊥α，则l∥β
  组卷：258引用：13难度：0.7

  解析

• 4．已知M、N分别是四面体OABC的棱OA，BC的中点，点P在线MN上，且MP=2PN，设向量

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，则

  OP

  =（　　）

  A． 1 6 a + 1 6 b + 1 6 c	B． 1 3 a + 1 3 b + 1 3 c
  C． 1 6 a + 1 3 b + 1 3 c	D． 1 3 a + 1 6 b + 1 6 c
  组卷：673引用：17难度：0.7

  解析

• 5．已知空间四面体ABCD的每条边长都等于a,点E、F分别是BC、AD的中点，则

  AE

  •

  AF

  的值为（　　）

  A．a2

  B． 1 2 a2

  C． 1 4 a2

  D． 3 4 a2
  组卷：279引用：23难度：0.6

  解析

• 6．在三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=PB=PC，M，N分别为AC，AB的中点，则异面直线PN和BM所成角的余弦值为（　　）

  A． - 6 6

  B． - 3 6

  C． 6 6

  D． 3 6
  组卷：129引用：9难度：0.6

  解析

• 7．如图，在直三棱柱ABC-A₁B₁C₁中，已知∠ABC=90°，P为侧棱CC₁上任意一点，Q为棱AB上任意一点，PQ与AB所成角为α，PQ与平面ABC所成的角为β，则α与β的大小关系为（　　）

  A．α=β

  B．α＜β

  C．α＞β

  D．不能确定
  组卷：177引用：4难度：0.8

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

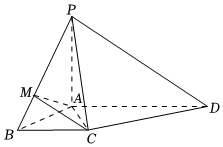• 21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，∠BAD=

  2

  π

  3

  ，AD=2AB=2BC=2PA=4，M为PB上靠近B的三等分点．
  （1）求证：PD∥平面ACM；
  （2）求直线PD与平面ACM的距离．
  组卷：60引用：2难度：0.4

  解析

• 22．如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是边长为2的正方形，PD=DC，F，G分别是PB，AD的中点．
  （1）求证：GF⊥平面PCB；​
  （2）在线段AP上是否存在一点M，使得DM与平面ADF所成角为30°？若存在，求出M点坐标，若不存在，请说明理由．
  组卷：40引用：1难度：0.4

  解析