2022-2023学年江苏省淮安市淮安区高二（下）期中数学试卷

一．单项选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。）

• 1．四名师范生从A，B，C三所学校中任选一所进行教学实习，其中A学校必有师范生去，则不同的选法方案有（　　）

  A．37种

  B．65种

  C．96种

  D．108种
  组卷：376引用：3难度：0.8

  解析

• 2．已知

  a

  =

  （

  2

  x

  ,

  1

  ，

  3

  ）

  ，

  b

  =

  （

  1

  ，

  3

  ，

  9

  ）

  ，如果

  a

  与

  b

  为共线向量，则x=（　　）

  A．1

  B． 1 2

  C． 1 3

  D． 1 6
  组卷：550引用：7难度：0.9

  解析

• 3．（2-x）⁵展开式中的第三项为（　　）

  A．10x2

  B．40x3

  C．-40x3

  D．80x2
  组卷：13引用：3难度：0.9

  解析

• 4．将4个6和2个8随机排成一行，则2个8不相邻的情况有（　　）

  A．480种

  B．240种

  C．15种

  D．10种
  组卷：417引用：4难度：0.7

  解析

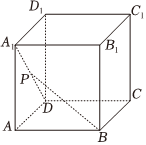• 5．如图，正方体ABCD-A₁B₁C₁D₁中，P是A₁D的中点，给出下列结论：
  ①PB∥D₁C；②PB∥平面B₁D₁C；③PB⊥B₁C；④PB⊥平面A₁C₁D；
  其中正确的结论个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：220引用：3难度：0.5

  解析

• 6．从3，5，7，11这四个质数中，每次取出两个不同的数，分别记为a,b,则共可得到

  a

  b

  的不同值的个数为（　　）

  A．6

  B．8

  C．12

  D．16
  组卷：42引用：2难度：0.8

  解析

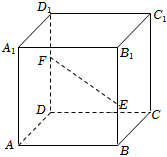• 7．如图，在平行六面体ABCD-A₁B₁C₁D₁中，E，F分别在棱BB₁和DD₁上，且

  DF

  =

  1

  2

  D

  D

  1

  ．记

  EF

  =

  x

  AB

  +

  y

  AD

  +

  z

  A

  A

  1

  ，若

  x

  +

  y

  +

  z

  =

  1

  4

  ，则

  BE

  B

  B

  1

  =（　　）

  A． 1 2

  B． 1 4

  C． 1 3

  D． 1 6
  组卷：109引用：9难度：0.8

  解析

四．解答题：（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步棸。）

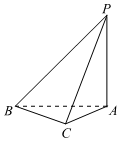• 21．在①PA⊥平面ABC，②BC⊥AC，③PB⊥BC三个条件中选两个条件补充在下面横线处，使得BC⊥平面PAC成立，请说明理由，并在此条件下进一步解答该题．
  如图，在三棱锥P-ABC中，若_____，且PA=2AC=BC=2，求直线AB与平面PBC所成角的正弦值．
  组卷：15引用：3难度：0.5

  解析

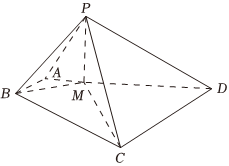• 22．如图，在四棱锥P-ABCD中，AP⊥DP，AB=1，AP=2，

  DP

  =

  2

  3

  ，CD=3，AB∥CD，AB⊥平面PAD，点M满足

  AM

  =

  λ

  AD

  （

  0

  ＜

  λ

  ＜

  1

  ）

  ．
  （1）若

  λ

  =

  1

  4

  ，求证：平面PBM⊥平面PCM；
  （2）设平面MPC与平面PCD的夹角为θ，若

  tanθ

  =

  7

  6

  ，求λ的值．
  组卷：585引用：3难度：0.3

  解析