当前位置：试卷中心 > 试卷详情

2023年山东省德州市高考数学三模试卷

发布：2024/5/25 8:0:9

一、选择题（本题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项

1．已知集合A={x|x²-4≤0}，B={x||x-a|＜1}，若B⊆A，则a的取值范围是（　　）
A．（-1，1） B．[-1，1] C．[-1，1） D．（-1，1]
组卷：517引用：3难度：0.8
解析
2．若复数z满足
z
+
z
＜
0
（
z
-
z
）
i
3
＜
0
，其中i为虚数单位，则z在复平面内对应的点在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：40引用：3难度：0.8
解析
3．已知命题p：x=-1是命题q：向量
a
=（1，x）与
b
=（x+2，x）共线的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：130引用：7难度：0.9
解析
4．函数
f
（
x
）
=
xln
|
x
|
e
x
-
e
-
x
的图象大致是（　　）
A． B． C． D．
组卷：160引用：9难度：0.7
解析
5．2023年1月底，人工智能研究公司OpenAI发布的名为“ChatGPT”的人工智能聊天程序进入中国，迅速以其极高的智能化水平引起国内关注．深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的，在神经网络优化中，指数衰减的学习率模型为
L
=
L
0
D
G
G
0
，其中L表示每一轮优化时使用的学习率，L₀表示初始学习率，D表示衰减系数，G表示训练迭代轮数，G₀表示衰减速度．已知某个指数衰减的学习率模型的初始学习率为0.8，衰减速度为12，且当训练迭代轮数为12时，学习率衰减为0.5．则学习率衰减到0.4以下（不含0.4）所需的训练迭代轮数至少为（参考数据：lg2≈0.3010）（　　）
A．16 B．17 C．18 D．19
组卷：150引用：2难度：0.5
解析
6．若（2x-3）¹²=a₀+a₁（x-1）+a₂（x-1）²+⋯+a₁₁（x-1）¹¹+a₁₂（x-1）¹²，则（　　）
A．a₀=-1
B．
a
0
-
a
1
+
a
2
-
a
3
+
…
+
a
10
-
a
11
+
a
12
=
-
3
12
C．a₁+a₂+…+a₁₂=-2
D．
a
1
2
+
a
2
2
2
+
…
+
a
11
2
11
+
a
12
2
12
=
-
1
组卷：272引用：3难度：0.5
解析
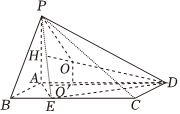7．在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=1，AB=2，AD=3，点E为BC上靠近B的三等分点，则三棱锥P-ADE外接球的表面积为（　　）
A．11π B．12π C．14π D．16π
组卷：164引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.）

21．已知F₁，F₂分别为双曲线
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左，右焦点，点
P
（
2
，
2
6
）
在C上，且双曲线C的渐近线与圆x²+y²-6y+8=0相切．
（1）求双曲线C的方程；
（2）若过点F₂且斜率为k的直线l交双曲线C的右支于A，B两点，Q为x轴上一点，满足|QA|=|QB|，试问
|
A
F
1
|
+
|
B
F
1
|
-
4
|
Q
F
2
|
是否为定值？若是，求出该定值；若不是，请说明理由．
组卷：149引用：2难度：0.3
解析
22．已知函数
f
（
x
）
=
lnx
+
1
2
（
a
-
x
）
2
，其中a∈R．
（1）当a=1时，求函数f（x）在（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性；
（3）若f（x）存在两个极值点x₁，x₂（x₁＜x₂），|f（x₂）-f（x₁）|的取值范围为
（
3
4
-
ln
2
，
15
8
-
2
ln
2
）
，求a的取值范围．
组卷：215引用：3难度：0.5
解析