当前位置：试卷中心 > 试卷详情

2023-2024学年广东省佛山市南海外国语学校八年级（上）月考数学试卷（10月份）

发布：2024/9/17 9:0:8

一．选择题（本大题共10小题，每小题3分，共30分）

1．25的算术平方根是（　　）
A．-5 B．±5 C．25 D．5
组卷：2647引用：21难度：0.9
解析
2．下列各组数中，是勾股数的是（　　）
A．
3
2
，2，
5
2
B．
2
，
3
，
5
C．1，1，2 D．9，12，15
组卷：162引用：2难度：0.8
解析
3．在6，-21.54，0，π，
22
7
，0.1010010001…（每相邻两个1之间0的个数依次增加1）这些数中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：281引用：9难度：0.8
解析
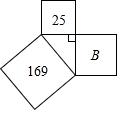4．如图，已知两正方形的面积分别是25和169，则字母B所代表的正方形的面积是（　　）
A．12 B．13 C．144 D．194
组卷：4603引用：38难度：0.9
解析
5．下列说法中，错误的是（　　）
A．1的平方根是1
B．0的平方根和立方根都是0
C．-1的立方根是-1
D．负数没有平方根
组卷：448引用：3难度：0.9
解析
6．若
a
是最简二次根式，则a的值可能是（　　）
A．-2 B．2 C．
3
2
D．8
组卷：873引用：15难度：0.8
解析
7．下列条件中，不能判断△ABC是直角三角形的是（　　）
A．∠A：∠B：∠C=3：4：5 B．∠A-∠B=∠C
C．AB：BC：AC=1：2：
3
D．AB=0.7，BC=2.4，AC=2.5
组卷：294引用：6难度：0.8
解析
8．下列各式中，正确的是（　　）
A．
（
-
2
）
2
=
-
2
B．
（
-
3
）
2
=
9
C．
3
-
9
=
-
3
D．
±
9
=±
3
组卷：1431引用：45难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

五．解答题（三）（本大题共2小题，每小题12分，共24分）

23．勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1），后人称之为“赵爽弦图”，流传至今．

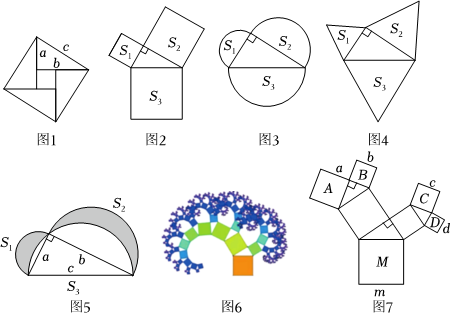
（1）①如图2，3，4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，面积分别为S₁，S₂，S₃，利用勾股定理，判断这3个图形中面积关系满足S₁+S₂=S₃的有
个．
②如图5，分别以直角三角形三边为直径作半圆，设图中两个月牙形图案（图中阴影部分）的面积分别为S₁，S₂，直角三角形面积为S₃，也满足S₁+S₂=S₃吗？若满足，请证明；若不满足，请求出S₁，S₂，S₃的数量关系．
（2）如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m,四个小正方形A，B，C，D的边长分别为a,b,c,d,则a²+b²+c²+d²=
．
组卷：662引用：4难度：0.6
解析
24．阅读材料：黑白双雄，纵横江湖；双剑合璧，天下无敌．这是武侠小说中的常见描述，其意是指两个人合在一起，取长补短，威力无比，在二次根式中也有这种相辅相成的“对子”，如
（
5
+
3
）
（
5
-
3
）
=
-
4
，
（
3
+
2
）
（
3
-
2
）
=
1
，它们的积不含根号，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式，于是，二次根式除法可以这样解：如
1
3
=
1
×
3
3
×
3
=
3
3
，
2
+
3
2
-
3
=
（
2
+
3
）
（
2
+
3
）
（
2
-
3
）
（
2
+
3
）
=
7
+
4
3
．像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫分母有理化．
解决问题：
（1）比较大小：
1
6
-
2

1
5
-
3
（用“＞”“＜”或“=”填空）；
（2）计算：
2
3
+
3
+
2
5
3
+
3
5
+
2
7
5
+
5
7
+
…
+
2
99
97
+
97
99
；
（3）设实数x,y满足
（
x
+
x
2
+
2023
）
（
y
+
y
2
+
2023
）
=
2023
，求x+y+2023的值．
组卷：260引用：2难度：0.5
解析