2023年江苏省扬州市中考数学试卷

一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将该选项的字母代号填涂在答题卡相应位置上）

• 1．实数-3的绝对值是（　　）

  A．-3

  B．3

  C． 1 3

  D．±3
  组卷：331引用：6难度：0.9

  解析

• 2．若（　　）•2a²b=2a³b,则括号内应填的单项式是（　　）

  A．a

  B．2a

  C．ab

  D．2ab
  组卷：1157引用：15难度：0.8

  解析

• 3．空气的成分（除去水汽、杂质等）是：氮气约占78%，氧气约占21%，其他微量气体约占1%．要反映上述信息，宜采用的统计图是（　　）

  A．条形统计图	B．折线统计图
  C．扇形统计图	D．频数分布直方图
  组卷：1119引用：26难度：0.8

  解析

• 4．下列图形是棱锥侧面展开图的是（　　）

  A．

  B．

  C．

  D．
  组卷：1001引用：6难度：0.8

  解析

• 5．已知a=

  5

  ，b=2，c=

  3

  ，则a、b、c的大小关系是（　　）

  A．b＞a＞c

  B．a＞c＞b

  C．a＞b＞c

  D．b＞c＞a
  组卷：1919引用：13难度：0.9

  解析

• 6．函数y=

  1

  x

  2

  的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：1646引用：8难度：0.5

  解析

• 7．在△ABC中，∠B=60°，AB=4，若△ABC是锐角三角形，则满足条件的BC长可以是（　　）

  A．1

  B．2

  C．6

  D．8
  组卷：1276引用：3难度：0.6

  解析

• 8．已知二次函数y=ax²-2x+

  1

  2

  （a为常数，且a＞0），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当x＜0时，y随x的增大而减小；④当x＞0时，y随x的增大而增大．其中所有正确结论的序号是（　　）

  A．①②

  B．②③

  C．②

  D．③④
  组卷：3922引用：14难度：0.5

  解析

二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

• 9．扬州市大力推进城市绿化发展，2022年新增城市绿地面积约2345000平方米，数据2345000用科学记数法表示为

  ．
  组卷：251引用：6难度：0.8

  解析

三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

• 27．【问题情境】
  在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A′D′C，∠ADB=∠A′D′C=90°，∠B=∠C=30°，设AB=2．
  【操作探究】
  如图1，先将△ADB和△A′D′C的边AD、A′D′重合，再将△A′D′C绕着点A按顺时针方向旋转，旋转角为α（0°≤α≤360°），旋转过程中△ADB保持不动，连接BC．
  （1）当α=60°时，BC=

  ；当BC=2

  2

  时，α=

  °；
  （2）当α=90°时，画出图形，并求两块三角板重叠部分图形的面积；
  （3）如图2，取BC的中点F，将△A′D′C′绕着点A旋转一周，点F的运动路径长为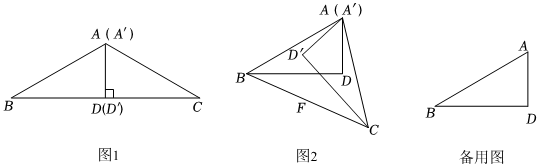

  ．
  
  组卷：2959引用：7难度：0.1

  解析

• 28．在平面直角坐标系xOy中，已知点A在y轴正半轴上．
  （1）如果四个点（0，0）、（0，2）、（1，1）、（-1，1）中恰有三个点在二次函数y=ax²（a为常数，且a≠0）的图象上．
  ①a=

  ；
  ②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；
  ③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n,试探究n-m是否为定值．如果是，求出这个值；如果不是，请说明理由．
  （2）已知正方形ABCD的顶点B、D在二次函数y=ax²（a为常数，且a＞0）的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式．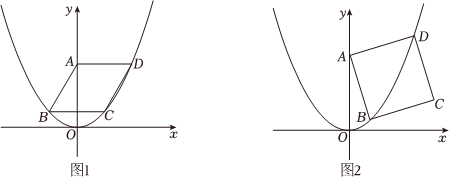
  
  组卷：3149引用：6难度：0.1

  解析