当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省名校联合体高二（下）第一次联考数学试卷

发布：2024/7/12 8:0:9

1．已知复数z满足
z
=
3
+
i
1
+
i
，其中 i是虚数单位，则|z|=（　　）
A．
2
B．
3
C．
5
D．
10
组卷：80引用：2难度：0.7
解析
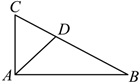2．如图，在△ABC中，
AB
=
6
，
AC
=
3
，
∠
BAC
=
π
2
，
BD
=
2
DC
，则
AB
•
AD
=（　　）
A．9 B．18 C．6 D．12
组卷：731引用：7难度：0.5
解析
3．
（
1
x
-
2
）
（
1
-
2
x
）
4
的展开式中，常数项为（　　）
A．-10 B．-8 C．-6 D．-4
组卷：399引用：4难度：0.7
解析
4．在平面直角坐标系中，已知点P（3，4）为角α终边上的点，则cos2α+cosα=（　　）
A．
8
25
B．
13
25
C．
22
25
D．
27
25
组卷：211引用：3难度：0.7
解析
5．已知等比数列{a_n}的各项均为不等于1的正数，数列{b_n}满足b_n=lga_n，b₃=18，b₆=12，则数列{b_n}前n项和的最大值等于（　　）
A．126 B．130 C．132 D．134
组卷：159引用：19难度：0.9
解析

6．现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动，有翻译、导游、礼仪、司机四项工作可以安排，以下说法正确的是（　　）

A．每人都安排一项工作的不同方法数为5⁴

B．每人都安排一项工作，每项工作至少有一人参加，则不同的方法数为480

C．如果司机工作不安排，其余三项工作至少安排一人，则这5名同学全部被安排的不同方法数为300

D．每人都安排一项工作，每项工作至少有一人参加，甲、乙不会开车但能从事其他三项工作，丙、丁、戊都能胜任四项工作，则不同安排方案的种数是126

组卷：44引用：2难度：0.6

21．设函数f（x）=（x+1）ln（x+1）．
（1）求曲线y=f（x）在点（e-1，f（e-1））处的切线方程；
（2）若对所有的x≥0，都有f（x）≥ax成立，求实数a的取值范围．
组卷：26引用：2难度：0.5
解析
22．设函数f（x）=e^2x-alnx.
（Ⅰ）讨论f（x）的导函数f′（x）零点的个数；
（Ⅱ）证明：当a＞0时，f（x）≥2a+aln
2
a
．
组卷：9702引用：20难度：0.3
解析