当前位置：试卷中心 > 试卷详情

2023-2024学年湖南师大附中梅溪湖中学九年级（上）入学数学试卷

发布：2024/9/7 16:0:8

一、选择题（本大题共10个小题，每小题3分，共30分）

1．下列方程中，属于一元二次方程的是（　　）
A．x²-2x-3=0 B．x²-xy=2 C．
x
2
+
1
x
=
2
D．2（x-1）=x
组卷：133引用：9难度：0.8
解析
2．点P（1，3）在正比例函数y=kx（k≠0）的图象上，则k的值为（　　）
A．
1
3
B．2 C．3 D．4
组卷：537引用：6难度：0.5
解析
3．在▱ABCD中，若∠A+∠C=140°，则∠B的度数是（　　）
A．70° B．110° C．120° D．140°
组卷：212引用：4难度：0.5
解析
4．将直线y=2x向下平移1个单位得到的直线是（　　）
A．y=-2x+1 B．y=-2x-1 C．y=2x+1 D．y=2x-1
组卷：414引用：6难度：0.5
解析
5．某企业参加“科技创新企业百强”评选，创新能力、创新价值、创新影响三项得分分别为8分，9分，7分，若将三项得分依次按5：3：2的比例计算总成绩，则该企业的总成绩为（　　）
A．8分 B．8.1分 C．8.2分 D．8.3分
组卷：752引用：10难度：0.8
解析
6．已知关于x的方程x²-2x+m=0有两个相等实数根，则m的值为（　　）
A．3 B．2 C．1 D．0
组卷：305引用：2难度：0.5
解析
7．在平面直角坐标系xOy中，点A（2，y₁），B（3，y₂）在函数y=-3x的图象上，则（　　）
A．y₁＞y₂ B．y₁=y₂
C．y₁＜y₂ D．以上都有可能
组卷：389引用：5难度：0.5
解析
8．如图，在平面直角坐标系xOy中，四边形ABCD是菱形，∠ABC=120°，点B的坐标为（0，-3），则点A的坐标为（　　）
A．
（
-
3
3
，
0
）
B．（3
3
，0） C．（-6，0） D．（6，0）
组卷：1506引用：11难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9个小题，第17、18、19题每题6分，第20、21题每题8分，第22、23题每题9第分，第24、25题每题10分，共72分）

24．著名数学家高斯曾说过：“如果别人思考数学的真理像我一样深入持久，他也会找到我的发现”，我们向伟人看齐，将这种勤思善学、砺能笃行的精神运用于日常的数学学习中来，尝试发现新的惊喜．
【提出问题】
我们曾探究过一元二次方程根与系数的关系，如果一元二次方程的系数按照某种规律发生变化，原方程的根与新方程的根是否也会产生某种联系？
【构造关系】
将一元二次方程的二次项系数、一次项系数和常数项按照n：1：
1
n
的比例放大或缩小，其中n≠0，我们称新方程为原方程的“系变方程”，系变倍数为n.
（1）当系变倍数为3时，求解一元二次方程x²+2x-3=0的“系变方程”．
【自能探究】
（2）已知某一元二次方程有两个实数根x₁，x₂，当n=2时，其“系变方程”也有两个实数根p、q,且x₁x₂=1，求
q
p
+
p
q
-（
4
p
+
1
4
q
）+17的最小值．
（3）已知关于x的方程（3x²+tx-2）²+（-2x²-tx+3）²=（x²+1）²有四个实数根x₁、x₂、x₃、x₄，问是否存在定值k,对于任意实数t,都满足
x
1
x
2
=
x
3
x
4
=k,若存在，请求出k的值；若不存在，请说明理由．
组卷：275引用：2难度：0.5
解析
25．如图，在平面直角坐标系中，平行四边形OABC中点A的坐标为（-3，-4），点B坐标为（6，-4），AB与y轴交于点M，点D是射线OC上一动点，点E是OD的中点，连接AE交y轴于点F，过点D作DG⊥OC交AE延长线于点G，交AB于点H，连接OG．

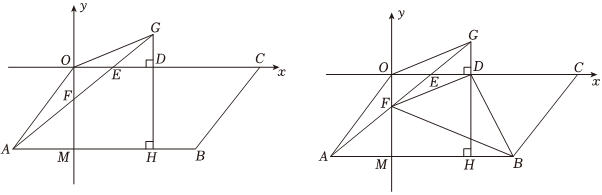
（1）若OD=4，求OG的长．
（2）若∠OAE=2∠GOE-∠GED，求OD的长．
（3）①连接DF，问直线DF是否经过一定点，若经过，请求出该定点；若不经过，请说明理由；
②连接FB，BD，若∠DFB=30°，求OD的长．
组卷：70引用：2难度：0.2
解析