著名数学家高斯曾说过：“如果别人思考数学的真理像我一样深入持久，他也会找到我的发现”，我们向伟人看齐，将这种勤思善学、砺能笃行的精神运用于日常的数学学习中来，尝试发现新的惊喜．
【提出问题】
我们曾探究过一元二次方程根与系数的关系，如果一元二次方程的系数按照某种规律发生变化，原方程的根与新方程的根是否也会产生某种联系？
【构造关系】
将一元二次方程的二次项系数、一次项系数和常数项按照n：1：1n的比例放大或缩小，其中n≠0，我们称新方程为原方程的“系变方程”，系变倍数为n.
（1）当系变倍数为3时，求解一元二次方程x2+2x-3=0的“系变方程”．
【自能探究】
（2）已知某一元二次方程有两个实数根x1，x2，当n=2时，其“系变方程”也有两个实数根p、q,且x1x2=1，求qp+pq-（4p+14q）+17的最小值．
（3）已知关于x的方程（3x2+tx-2）2+（-2x2-tx+3）2=（x2+1）2有四个实数根x1、x2、x3、x4，问是否存在定值k,对于任意实数t,都满足x1x2=x3x4=k,若存在，请求出k的值；若不存在，请说明理由．
1
n
q
p
p
q
4
p
1
4
q
x
1
x
2
x
3
x
4
【答案】（1）x1=-1，；（2）；（3）k=或，理由见解析．
x
2
=
1
3
15
16
2
3
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 16:0:8组卷：298引用：2难度：0.5
相似题
-
1．已知关于x的方程mx2-（m+2）x+2=0．
（Ⅰ）证明：不论m为何值时，方程总有实数根．
（Ⅱ）m为何整数时，方程有两个不相等的正整数根．发布：2025/6/18 14:30:2组卷：1465引用：94难度：0.5 -
2．关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根．
（1）求m的取值范围；
（2）若x1，x2是一元二次方程x2+2x+2m=0的两个根，且+x21=8，求m的值．x22发布：2025/6/18 16:30:1组卷：2122引用：45难度：0.5 -
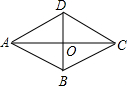3．如图，菱形ABCD的边长是5，两条对角线交于O点，且AO、BO的长分别是关于x的方程x2+（2m-1）x+m2+3=0的根，则m的值为（ ）发布：2025/6/18 14:30:2组卷：1032引用：30难度：0.7
