2022-2023学年陕西省西安市鄠邑区高二（下）期末数学试卷（理科）

一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

• 1．若a∈R，z满足z（1+i）=a+2i,且z为纯虚数，则a=（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：52引用：2难度：0.9

  解析

• 2．下列导数运算正确的是（　　）

  A． （ sin π 3 ） ′ = cos π 3	B． （ ln （ - x ） ） ′ = - 1 x
  C．[（2e）x]'=（2e）x	D． （ x ） ′ = 1 2 x
  组卷：41引用：1难度：0.8

  解析

• 3．

  ∫

  1

  0

  1

  -

  x

  2

  dx

  =

  （　　）

  A． π 4

  B． π 2

  C． 1 2

  D． 1 4
  组卷：138引用：8难度：0.9

  解析

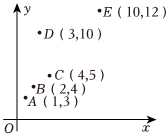• 4．有一散点图如图所示，在5个数据（x,y）中去掉D（3，10）后，下列说法正确的是（　　）

  A．相关系数r变小

  B．残差平方和变小

  C．变量x,y负相关

  D．解释变量x与预报变量y的相关性变弱
  组卷：36引用：7难度：0.7

  解析

• 5．

  -

  1

  x

  2

  （

  1

  +

  ay

  ）

  6

  展开式中x^-2y³项的系数为160，则a=（　　）

  A．2

  B．4

  C．-2

  D． - 2 2
  组卷：30引用：2难度：0.7

  解析

• 6．用反证法证明命题“平面四边形四个内角中至少有一个不大于90°”时，应假设（　　）

  A．四个内角都大于90°

  B．四个内角都不大于90°

  C．四个内角至多有一个大于90°

  D．四个内角至多有两个大于90°
  组卷：89引用：4难度：0.8

  解析

• 7．随机变量ξ的分布列如表，若E（ξ）=0，则D（ξ）=（　　）
  

  ξ	-3	0	3
  P	1 3	a	b

  A．6

  B．2

  C．0

  D． 6
  组卷：299引用：3难度：0.9

  解析

三、解答题（本大题共6小题，满分70分，解答应写出必要的文字说明、证明过程或演算步骤．）

• 21．某运动员射击一次所得环数X的分布列如下：
  

  X	8	9	10
  P	0.4	0.4	0.2

  现进行两次射击，且两次射击互不影响，以该运动员两次射击中最高环数作为他的成绩，记为ξ．
  （1）求该运动员两次命中的环数相同的概率；
  （2）求ξ的分布列和数学期望Eξ．
  组卷：94引用：3难度：0.8

  解析

• 22．已知函数f（x）=xcosx.
  （1）当x∈（0，π）时，求证：f（x）＜sinx；
  （2）证明：w（x）=f'（x）在

  （

  0

  ，

  π

  2

  ）

  上单调递减；
  （3）求证：当

  x

  ∈

  （

  0

  ，

  π

  2

  ）

  时，方程

  f

  （

  x

  ）

  -

  1

  2

  =

  0

  有且仅有2个实数根．
  组卷：23引用：1难度：0.5

  解析