2022-2023学年北京八十中睿德分校九年级(上)期中数学试卷
发布:2024/9/12 0:0:8
一、选择题(每题3分,共24分)
-
1.下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是( )
组卷:590引用:40难度:0.8 -
2.一元二次方程2x2+x-5=0的二次项系数、一次项系数、常数项分别是( )
组卷:1423引用:34难度:0.8 -
3.把抛物线y=x2向上平移3个单位,得到的抛物线是( )
组卷:257引用:11难度:0.7 -
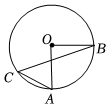 4.如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( )组卷:317引用:5难度:0.5
4.如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( )组卷:317引用:5难度:0.5 -
5.用配方法解方程x2+4x=1,变形后结果正确的是( )
组卷:155引用:19难度:0.6 -
6.点A(-2,y1)、B(1,y2)在二次函数y=x2+2x-1的图象上,y1与y2的大小关系是( )
组卷:525引用:4难度:0.6 -
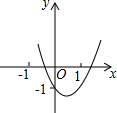 7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )组卷:191引用:9难度:0.7
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )组卷:191引用:9难度:0.7 -
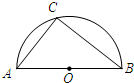 8.如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )组卷:1270引用:26难度:0.9
8.如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )组卷:1270引用:26难度:0.9
二、填空题(每题3分,共24分)
-
9.写出一个开口向下的抛物线的解析式
.组卷:55引用:4难度:0.7
三、解答题(17-20题每题4分,21-26题每题5分,27题每题6分,共52分)
-
26.已知∠AOB=30°,H为射线OA上一定点,OH=
+1,P为射线OB上一点,M为线段OH上一动点,连接PM,满足∠OMP为钝角,以点P为中心,将线段PM顺时针旋转150°,得到线段PN,连接ON.3
(1)依题意补全图1;
(2)求证:∠OMP=∠OPN;
(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.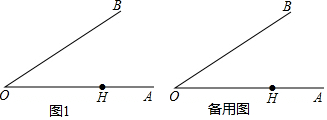 组卷:4720引用:7难度:0.4
组卷:4720引用:7难度:0.4 -
27.对于平面直角坐标系xOy中的点A和点P,若将点P绕点A逆时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”,图1为点P关于点A的“垂链点”Q的示意图.
(1)已知点A的坐标为(0,0),点P关于点A的“垂链点”为点Q;
①若点P的坐标为(2,0),则点Q的坐标为 .
②若点Q的坐标为(-2,1),则点P的坐标为 .
(2)如图2,已知点C的坐标为(1,0),点D在直线y=x+1上,若点D关于点C的“垂链点”在坐标轴上,试求出点D的坐标.13
(3)如图3,已知图形G是端点为(1,0)和(0,-2)的线段,图形H是以点O为中心,各边分别与坐标轴平行的边长为6的正方形,点M为图形G上的动点,点N为图形H上的动点,若存在点T(0,t),使得点M关于点T的“垂链点”恰为点N,请直接写出t的取值范围.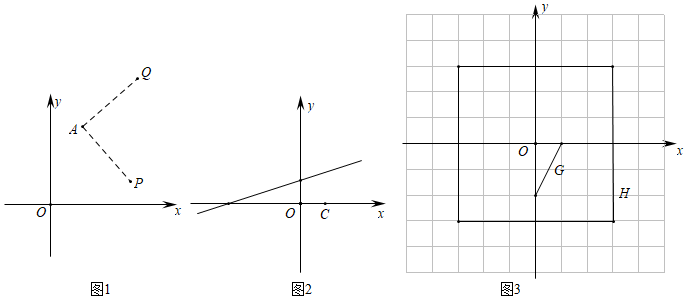 组卷:1397引用:3难度:0.1
组卷:1397引用:3难度:0.1


