2022-2023学年青海省西宁市海湖中学高二（下）期中数学试卷（文科）

一、选择题（本大题共12小题，每小题5分，共60分）

• 1．在一次联考后，某校对甲、乙两个文科班的数学考试成绩进行分析，规定：大于或等于120分为优秀，120分以下为非优秀，统计成绩后，得到如下2×2列联表：
  

  	优秀	非优秀	合计
  甲班	10	50	60
  乙班	20	30	50
  合计	30	80	110

  附：X²=

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  α	0.05	0.01	0.005	0.001
  xα	3.841	6.635	7.879	10.828

  根据独立性检验，可以认为数学考试成绩与班级有关系的把握为（　　）

  A．95%

  B．99.5%

  C．99.9%

  D．99%
  组卷：44引用：2难度：0.8

  解析

• 2．下列推理过程是类比推理的为（　　）

  A．科学家通过研究蝙蝠的声波发明了雷达

  B．人们通过实验得出投骰子出现数字1的概率为 1 6

  C．数列a1=1，a2=2，a3=3，推理出a4=4

  D．教室的几把椅子坏了，那么该教室内所有的椅子都坏了
  组卷：3引用：1难度：0.7

  解析

• 3．设复数z满足z+i=4-i,则

  z

  4

  +

  2

  i

  =（　　）

  A．4-2i

  B．4+2i

  C． 3 + 4 i 5

  D． 3 - 4 i 5
  组卷：85引用：7难度：0.8

  解析

• 4．若i（1-z）=1，则z+

  z

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：5651引用：18难度：0.9

  解析

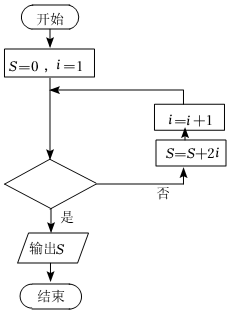• 5．执行如图所示的程序框图，若输出的S=30，则判断框中可填（　　）

  A．i≥5？

  B．i≥6？

  C．i＞6？

  D．i≥7？
  组卷：28引用：3难度：0.8

  解析

• 6．学校艺术节对同一类的A，B，C，D四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下：
  甲说：“A作品获得一等奖”；
  乙说：“C作品获得一等奖”；
  丙说：“B，D两项作品未获得一等奖”；
  丁说：“A或D作品获得一等奖”．
  评奖揭晓后发现这四位同学中只有两位预测正确，则获得一等奖的作品是（　　）

  A．A作品

  B．B作品

  C．C作品

  D．D作品
  组卷：31引用：2难度：0.5

  解析

• 7．直线l的参数方程为

  x = 1 + t

  y = 2 - 3 t

  （t为参数），则直线l的斜率为（　　）

  A．3

  B． 1 3

  C．- 1 3

  D．-3
  组卷：91引用：3难度：0.8

  解析

三、解答题（本大题共$6$小题，共70分。解答应写出文字说明，证明过程或演算步骤。）

• 21．已知曲线C的参数方程为

  x = 2 + 3 cosθ

  y = 3 sinθ

  （θ为参数，θ∈R），直线l经过P（0，-3）且倾斜角为

  π

  4

  ．
  （1）求曲线C的普通方程；
  （2）直线l与曲线C交于A，B两点，求|AB|的值．
  组卷：160引用：2难度：0.6

  解析

• 22．在平面直角坐标系xOy中，曲线C的参数方程为

  x = 3 cosα

  y = sinα

  （α为参数），在以原点O为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin

  （

  θ

  -

  π

  4

  ）

  =1．
  （1）求C的普通方程和l的倾斜角；
  （2）设点P（0，

  2

  ），直线l和C交于A，B两点，求|PA|+|PB|．
  组卷：48引用：3难度：0.5

  解析