当前位置：试卷中心 > 试卷详情

2022-2023学年贵州省贵阳市花溪区同为京学附属实验学校八年级（下）第三次月考数学试卷

发布：2024/9/5 9:0:8

1．下列图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：151引用：14难度：0.8
解析
2．已知一个不等式的解集在数轴上表示如图，则对应的不等式是（　　）
A．x-1＞0 B．x-1＜0 C．x+1＞0 D．x+1＜0
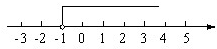组卷：555引用：11难度：0.9
解析
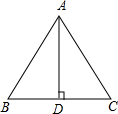3．如图，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是（　　）
A．∠B=45° B．∠BAC=90° C．BD=AC D．AB=AC
组卷：1008引用：7难度：0.9
解析
4．若分式
1
x
-
2
有意义，则x的取值范围是（　　）
A．x＞2 B．x≠2 C．x≠0 D．x≠-2
组卷：1133引用：31难度：0.9
解析
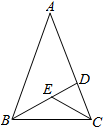5．如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）
A．5个 B．4个 C．3个 D．2个
组卷：8843引用：68难度：0.9
解析
6．不等式组
x
≥
3
x
＞
2
的解集在数轴上表示为（　　）
A． B． C． D．
组卷：1608引用：6难度：0.8
解析
7．下列因式分解正确的是（　　）
A．3x+3y+3=3（x+y） B．a²-4a+4=（a+2）²
C．x²-4y²=（x-4y）（x+4y） D．x²+2x=x（x+2）
组卷：366引用：4难度：0.7
解析

20．五一期间，某商场计划购进甲、乙两种商品，已知购进甲商品1件和乙商品3件共需240元；购进甲商品2件和乙商品1件共需130元．
（1）求甲、乙两种商品每件的进价分别是多少元？
（2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．
组卷：593引用：5难度：0.6
解析
21．【问题背景】
如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，试探究图中线段BE、EF、FD之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是
．
【探索延伸】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF=
1
2
∠BAD，上述结论是否仍然成立，并说明理由．
【学以致用】
如图3，四边形ABCD是边长为5的正方形，∠EBF=45°，直接写出△DEF的周长．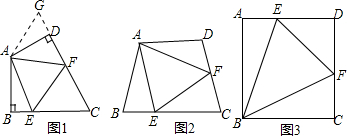
组卷：3837引用：14难度：0.5
解析