2022-2023学年安徽省滁州市定远中学高一（下）质检数学试卷（7月份）

一、单选题（本大题共8小题，共40分。在每小题列出的选项中，选出符合题目的一项）

• 1．若集合A={x||x|＜3}，B={x|x=2n+1，n∈Z}，则A∩B=（　　）

  A．（-1，1）

  B．（-3，3）

  C．{-1，1}

  D．{-3，-1，1，3}
  组卷：347引用：6难度：0.8

  解析

• 2．若复数z满足z+2

  z

  =3-i,则|z|=（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：6引用：2难度：0.8

  解析

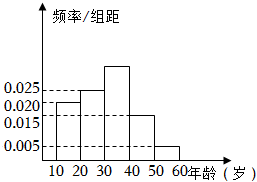• 3．随机抽取骑行共享单车的市民进行问卷调查，得到样本的频率分布直方图如图所示．再从这些市民中用分层抽样的方法抽取一个样本进行调查，若第二次抽取的样本中[30，40）年龄段的人数为14，则第二次抽取的样本中[50，60]年龄段的人数为（　　）

  A．2

  B．3

  C．5

  D．6
  组卷：12引用：3难度：0.8

  解析

• 4．某学校在校学生有3000人，为了增强学生的体质，学校举行了跑步和登山比赛，每人都参加且只参加其中一项比赛，高一、高二、高三年级参加跑步的人数分别为a,b,c,且a：b：c=2：3：4，全校参加登山的人数占总人数的

  2

  5

  ．为了了解学生对本次比赛的满意程度，按分层抽样的方法从中抽取一个容量为300的样本进行调查，则应从高二年级参加跑步的学生中抽取（　　）

  A．15人

  B．30人

  C．45人

  D．60人
  组卷：165引用：6难度：0.8

  解析

• 5．O为▱ABCD两条对角线的交点，

  AB

  =4

  e

  1

  ，

  BC

  =6

  e

  2

  ，则

  DO

  =（　　）

  A．2 e 1 + e 2

  B．2 e 1 - e 2

  C．2 e 1 +3 e 2

  D．2 e 1 -3 e 2
  组卷：83引用：6难度：0.8

  解析

• 6．已知m,n为两条不同的直线，α，β为两个不同的平面，则下列结论中正确的是（　　）

  A．若m∥α，m∥n,则n∥α

  B．若m∥α，n∥α，则m∥n

  C．若m∥α，m⊂β，α∩β=n,则m∥n

  D．若m∥α，n⊂α，则m∥n
  组卷：171引用：3难度：0.7

  解析

• 7．已知向量

  a

  =

  （

  4

  ，

  2

  m

  -

  3

  ）

  ，

  b

  =

  （

  m

  ,-

  5

  ）

  ，若

  a

  ⊥

  b

  ，则实数m=（　　）

  A．-5

  B．5

  C． - 5 2

  D． 5 2
  组卷：146引用：3难度：0.8

  解析

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

• 21．如图，四棱锥P-ABCD的底面是正方形，PA⊥平面ABCD，PA=AB．点E是PD的中点，作EF⊥PC，交PC于点F．
  （1）设平面PAB与平面ACE的交线为l,试判断直线PB与直线l的位置关系，并给出证明；
  （2）求平面PAB与平面ACE所成的较小的二面角的余弦值；
  （3）求直线PD与平面AEF所成角的正切值．
  组卷：266引用：3难度：0.5

  解析

• 22．在锐角△ABC中，角A，B，C所对的边分别是a,b,c,已知b=2，

  a

  b

  =

  3

  3

  sinC+cosC．
  （1）求角B；
  （2）若M是△ABC内的一动点，且满足

  BM

  =

  MA

  +

  MC

  ，则|

  BM

  |是否存在最大值？若存在，请求出最大值及取最大值的条件；若不存在，请说明理由；
  （3）若D是△ABC中AC上的一点，且满足

  BA

  •

  BD

  |

  BA

  |

  =

  BD

  •

  BC

  |

  BC

  |

  ，求AD：DC的取值范围．
  组卷：346引用：6难度：0.3

  解析