2023-2024学年江苏省南通市如皋市高三（上）期初调研数学试卷

一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

• 1．集合M={x|sinx=1}，N={x|cosx=0}，则下列说法正确的是（　　）

  A．M=N	B．M⊆N
  C．N⊆M	D．M，N关系不确定
  组卷：69引用：3难度：0.8

  解析

• 2．已知命题p：∀x∈[1，3]，x²-ax+3＜0，则p的一个必要不充分条件是（　　）

  A．a＜5

  B．a＞3

  C．a＜4

  D．a＞4
  组卷：383引用：10难度：0.7

  解析

• 3．设m,n,l是三条不同的直线，α，β，γ是三个不同的平面，有下列命题中，真命题为（　　）

  A．若m⊥n,n⊥l,则m⊥l	B．若α⊥β，β⊥γ，则α⊥γ
  C．若m⊥α，m∥n,则n⊥α	D．若m∥n,m∥α，则n∥α
  组卷：32引用：3难度：0.6

  解析

• 4．在△ABC中，

  AB

  ⊥

  AC

  ，且

  |

  AB

  |

  =

  |

  AC

  |

  =

  2

  ，M是BC的中点，O是线段AM的中点，则

  OA

  •

  （

  OB

  +

  OC

  ）

  的值为（　　）

  A．0

  B． - 3 2

  C． - 1 2

  D．2
  组卷：55引用：4难度：0.7

  解析

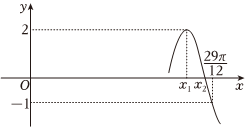• 5．已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示，且

  x

  2

  -

  x

  1

  =

  π

  4

  ，则ω，φ的值为（　　）

  A． ω = 1 ， φ = 3 π 4	B． ω = 1 ， φ = 11 π 12
  C． ω = 2 ， φ = π 3	D． ω = 2 ， φ = 2 π 3
  组卷：164引用：7难度：0.7

  解析

• 6．点P是曲线y=x²-lnx上任意一点，则点P到直线x-y-2=0的最短距离为（　　）

  A． 3

  B． 3 3 2

  C． 2 2 3

  D． 2
  组卷：90引用：4难度：0.7

  解析

• 7．已知数列{a_n}满足a₁=1，且a_n+1=a_n+2，数列{b_n}满足b₁=1，b_n+1-b_n=a_n+1，则

  b

  n

  +

  8

  n

  的最小值为（　　）

  A． 13 3

  B．5

  C． 4 2

  D． 17 3
  组卷：302引用：7难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知数列{a_n}是公差为3的等差数列，数列{b_n}是公比为2的等比数列，且满足a₁+a₃=b₁+b₂+b₃，a₂+a₄=b₂+b₄.将数列{a_n}与{b_n}的公共项按照由小到大的顺序排列，构成新数列{c_n}．
  （1）证明：c_n=b_2n；
  （2）求数列{a_nc_n}的前n项和S_n．
  组卷：118引用：4难度：0.4

  解析

• 22．已知函数f（x）=ae^x-x-a.
  （1）若f（x）≥0，求a的值；
  （2）证明：当a≥1时，f（x）＞xlnx-sinx成立．
  组卷：75引用：6难度：0.4

  解析