2023年青海省中考数学试卷
发布：2024/7/12 8:0:9
一、选择题（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项符合要求）．
-
1．青海地大物博，风光秀美，素有“大美青海”之美誉．下面四个艺术字中，不是轴对称图形的是（ ）
组卷：205引用：3难度：0.5 -
2．计算2+（-3）的结果是（ ）
组卷：1263引用：11难度：0.9 -
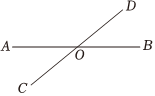3．如图，直线AB，CD相交于点O，∠AOD=140°，则∠AOC的度数是（ ）组卷：623引用：8难度：0.5 -
4．下列几何体中，主视图、左视图和俯视图都相同的是（ ）
组卷：380引用：5难度：0.5 -
5．下列运算正确的是（ ）
组卷：339引用：7难度：0.8 -
6．为了缅怀革命先烈，传承红色精神，青海省某学校八年级师生在清明节期间前往距离学校15km的烈士陵园扫墓．一部分师生骑自行车先走，过了30min后，其余师生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车师生速度的2倍，设骑车师生的速度为x km/h.根据题意，下列方程正确的是（ ）
组卷：1379引用：13难度：0.7 -
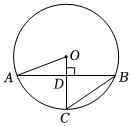7．如图，AB是⊙O的弦，C是⊙O上一点，OC⊥AB，垂足为D．若∠A=20°，则∠ABC=（ ）组卷：864引用：5难度：0.6 -
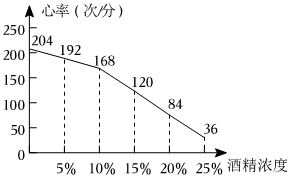8．生物兴趣小组探究酒精对某种鱼类的心率是否有影响，实验得出心率与酒精浓度的关系如图所示，下列说法正确的是（ ）组卷：541引用：5难度：0.8
三、解答题（本大题共9小题，共72分．解答应写出必要的文字说明、证明过程或演算步骤）
-
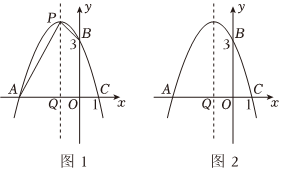24．如图，二次函数y=-x2+bx+c的图象与x轴相交于点A和点C（1，0），交y轴于点B（0，3）．
（1）求此二次函数的解析式；
（2）设二次函数图象的顶点为P，对称轴与x轴交于点Q，求四边形AOBP的面积（请在图1中探索）；
（3）二次函数图象的对称轴上是否存在点M，使得△AMB是以AB为底边的等腰三角形？若存在，请求出满足条件的点M的坐标；若不存在，请说明理由（请在图2中探索）．组卷：1712引用：7难度：0.2 -
25．综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆，车轮都是圆形的．为什么车轮要做成圆形的呢？这里面有什么数学道理吗？带着这样的疑问，小青做了如下的探究活动：
将车轮设计成不同的正多边形，在水平地面上模拟行驶．
（1）探究一：将车轮设计成等边三角形，转动过程如图1，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，BA=CA=DA=2，圆心角∠BAD=120°．此时中心轨迹最高点是C（即ˆBD的中点），转动一次前后中心的连线是BD（水平线），请在图2中计算C到BD的距离d1．ˆBD
（2）探究二：将车轮设计成正方形，转动过程如图3，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，BA=CA=DA=2，圆心角∠BAD=90°．此时中心轨迹最高点是C（即ˆBD的中点），转动一次前后中心的连线是BD（水平线），请在图4中计算C到BD的距离d2（结果保留根号）．ˆBD
（3）探究三：将车轮设计成正六边形，转动过程如图5，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，圆心角∠BAD=．ˆBD
此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是BD（水平线），在图6中计算C到BD的距离d3=（结果保留根号）．ˆBD
（4）归纳推理：比较d1，d2，d3大小：，按此规律推理，车轮设计成的正多边形边数越多，其中心轨迹最高点与转动一次前后中心连线（水平线）的距离 （填“越大”或“越小”）．
（5）得出结论：将车轮设计成圆形，转动过程如图7，其中心（即圆心）的轨迹与水平地面平行，此时中心轨迹最高点与转动前后中心连线（水平线）的距离d=.这样车辆行驶平稳、没有颠簸感．所以，将车轮设计成圆形．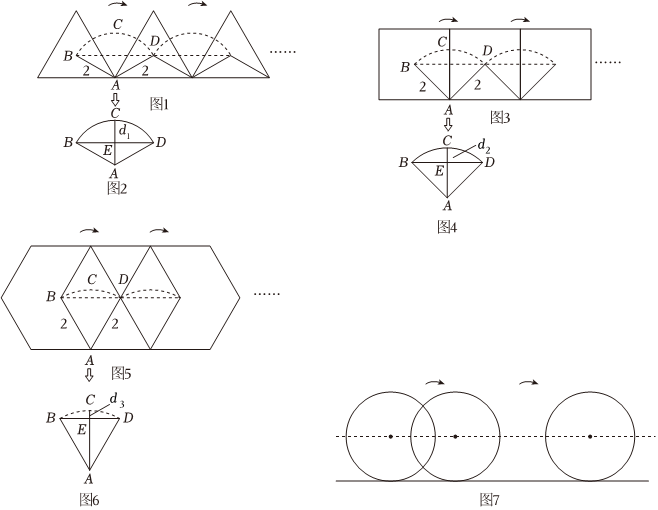
组卷：682引用：4难度：0.3
