2022-2023学年广东省梅州市丰顺县潭江中学九年级（上）月考数学试卷（9月份）
发布：2024/8/16 14:0:1
一、选择题（共10题，共30分）
-
1．如图，四边形ABCD是菱形，DH⊥AB于H，若AC=8，BD=6，则DH的长度为（ ）组卷：240引用：3难度：0.7 -
2．已知正方形ABCD的边长为，E为DC边上一点，∠EBC=30°，则BE的长为（ ）53组卷：6引用：1难度：0.6 -
3．如图，矩形纸片ABCD中，AD=4，AB=8，把纸片沿直线AC折叠，点B落在E处，AE交DC于点F，若DF=3，则EF的长为（ ）组卷：145引用：2难度：0.9 -
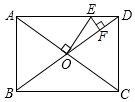4．如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为（ ）组卷：12366引用：80难度：0.4 -
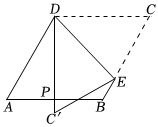5．如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）组卷：2960引用：107难度：0.9 -
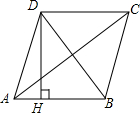6．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（ ）组卷：14263引用：100难度：0.5 -
7．矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AC=8，则△ABO的周长为（ ）
组卷：792引用：80难度：0.9 -
8．已知：如图，正方形ABCD中，AB=2，AC，BD相交于点O，E，F分别为边BC，CD上的动点（点E，F不与线段BC，CD的端点重合）．且BE=CF，连接OE，OF，EF．在点E，F运动的过程中，有下列四个说法：
①△OEF是等腰直角三角形；②△OEF面积的最小值是；12
③至少存在一个△ECF，使得△ECF的周长是2+；④四边形OECF的面积是1．3
其中正确的是（ ）组卷：870引用：8难度：0.6
三、解答题（共8小题，满分62分）
-
24．在▱ABCD中，点B关于AD的对称点为B′，连接AB′，CB′，CB′交AD于F点．
（1）如图1，∠ABC=90°，求证：FB′=FC；
（2）小宇通过观察、实验、提出猜想：如图2，在点B绕点A旋转的过程中，点F始终为CB′的中点．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：过点B作B'G∥CD交AD于G点，只需证三角形全等；
想法2：连接BB′交AD于H点，只需证H为BB′的中点；
想法3：连接BB′，BF，只需证∠B′BC=90°．FB′=FB=FC
……
请你参考上面的想法，证明F为CB′的中点．（一种方法即可）
（3）如图3，当∠ABC=135°时，AB′，CD的延长线相交于点E，求的值．CEAF
组卷：374引用：4难度：0.1 -
25．在平面直角坐标系xOy中，对于图形G，若存在一个正方形γ，这个正方形的某条边与x轴垂直，且图形G上的所有的点都在该正方形的内部或者边上，则称该正方形γ为图形G的一个正覆盖．很显然，如果图形G存在一个正覆盖，则它的正覆盖有无数个，我们将图形G的所有正覆盖中边长最小的一个，称为它的紧覆盖，如图所示，图形G为三条线段和一个圆弧组成的封闭图形，图中的三个正方形均为图形G的正覆盖，其中正方形ABCD就是图形G的紧覆盖．
（1）对于半径为2的⊙O，它的紧覆盖的边长为 ．
（2）如图1，点P为直线y=-2x+3上一动点，若线段OP的紧覆盖的边长为2，求点P的坐标．
（3）如图2，直线y=3x+3与x轴，y轴分别交于A，B，
①以O为圆心，r为半径的⊙O与线段AB有公共点，且由⊙O与线段AB组成的图形G的紧覆盖的边长小于4，直接写出r的取值范围；
②若在抛物线y=ax2+2ax-2（a≠0）上存在点C，使得△ABC的紧覆盖的边长为3，直接写出a的取值范围．
组卷：298引用：4难度：0.1
