2023-2024学年江苏省四校联盟高二（上）月考数学试卷（10月份）

一、单项选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．过两点A（3，y），B（2，0）的直线的倾斜角为120°，则y=（　　）

  A． 3 3

  B． 3

  C． - 3 3

  D． - 3
  组卷：325引用：6难度：0.8

  解析

• 2．抛物线y=ax²的准线方程是y=1，则a的值为（　　）

  A． 1 4

  B． - 1 4

  C．4

  D．-4
  组卷：121引用：23难度：0.9

  解析

• 3．已知直线l：kx-y-k+3=0，且无论k取何值，直线l与圆（x-5）²+（y-6）²=r²（r＞0）恒有公共点，则r的取值范围是（　　）

  A．[3，5]

  B．（3，+∞）

  C．[4，6）

  D．[5，+∞）
  组卷：45引用：8难度：0.7

  解析

• 4．如图，已知F₁，F₂分别是椭圆的左、右焦点，现以F₂为圆心作一个圆恰好经过椭圆的中心并且交椭圆于点M，N．若过点F₁的直线MF₁是圆F₂的切线，则椭圆的离心率为（　　）

  A． 3 - 1

  B． 2 - 3

  C． 2 2

  D． 3 2
  组卷：344引用：13难度：0.6

  解析

• 5．已知抛物线x²=4y的焦点为F，点B（1，3），若点A为抛物线任意一点，当|AB|+|AF|取最小值时，点A的坐标为（　　）

  A． （ 1 4 ， 1 ）

  B． （ 1 ， 1 4 ）

  C．（1，4）

  D．（4，1）
  组卷：156引用：4难度：0.7

  解析

• 6．定义焦点相同，且离心率互为倒数的椭圆和双曲线为一对相关曲线．已知F₁，F₂是一对相关曲线的焦点，P是这对相关曲线在第一象限的交点，则点P与以F₁F₂为直径的圆的位置关系是（　　）

  A．在圆外

  B．在圆上

  C．在圆内

  D．不确定
  组卷：51引用：4难度：0.6

  解析

• 7．若直线

  y

  =

  1

  2

  x

  +

  3

  的倾斜角为α，直线y=kx-5的倾斜角为3α，则k=（　　）

  A． 4 3

  B．5

  C． 9 2

  D． 11 2
  组卷：200引用：5难度：0.8

  解析

四、解答题（本大题共6小题，共70分.解答时应写出文字说明、证明过程或演算步骤）

• 21．已知点A（4，4），B（0，3），圆C的半径为1．
  （1）若圆C的圆心坐标为C（3，2），过点A作圆C的切线，求此切线的方程；
  （2）若圆C的圆心C在直线l：y=x-1上，且圆C上存在点M，使|MB|=2|MO|，O为坐标原点，求圆心C的横坐标a的取值范围．
  组卷：236引用：10难度：0.5

  解析

• 22．“工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动，在我国源远流长．某些折纸活动蕴含丰富的数学内容，例如：用一张圆形纸片，按如下步骤折纸（如图）
  
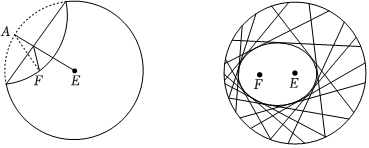
  步骤1：设圆心是E，在圆内异于圆心处取一点，标记为F；
  步骤2：把纸片折叠，使圆周正好通过点F；
  步骤3：把纸片展开，并留下一道折痕；
  步骤4：不停重复步骤2和3，就能得到越来越多的折痕．已知这些折痕所围成的图形是一个椭圆．若取半径为4的圆形纸片，设定点F到圆心E的距离为

  2

  3

  ，按上述方法折纸．
  （1）以点F、E所在的直线为x轴，建立适当的坐标系，求折痕围成的椭圆C的标准方程；
  （2）设椭圆C的下顶点为D，过点D作两条互相垂直的直线l₁，l₂，这两条直线与椭圆C的另一个交点分别为M，N．设l的斜率为k（k≠0），△DMN的面积为S，当

  S

  |

  k

  |

  ＞

  16

  9

  时，求k的取值范围．
  组卷：67引用：3难度：0.5

  解析