2022-2023学年广东省江门市台山市华侨中学高二（上）期中数学试卷

一、单选题(每小题5分,共40分)

• 1．若直线l过点（-1，2）且斜率

  k

  =

  -

  3

  2

  ，则l的方程为（　　）

  A．3x+2y-1=0

  B．2x+3y-1=0

  C．3x+2y+1=0

  D．2x-3y-1=0
  组卷：40引用：1难度：0.5

  解析

• 2．已知向量

  a

  =

  （

  -

  3

  ，

  2

  ，

  4

  ）

  ，

  b

  =

  （

  1

  ，-

  2

  ，

  2

  ）

  ，则

  |

  a

  -

  b

  |

  =（　　）

  A． 2 10

  B．40

  C．6

  D．36
  组卷：659引用：10难度：0.8

  解析

• 3．已知平面α的法向量为

  n

  =（2，-2，4），

  AB

  =（-1，1，-2），则直线AB与平面α的位置关系为（　　）

  A．AB⊥α	B．AB⊂α
  C．AB与α相交但不垂直	D．AB∥α
  组卷：788引用：10难度：0.8

  解析

• 4．若直线a²x-y+1=0与ax-y-2=0直线平行，则a的值为（　　）

  A．-1

  B．0

  C．1

  D．0或1
  组卷：12引用：2难度：0.7

  解析

• 5．已知平面α的一个法向量

  n

  =（-2，-2，1），点A（-1，3，0）在平面α内则点P（-2，1，4）到α的距离为（　　）

  A．10

  B．3

  C． 8 3

  D． 10 3
  组卷：498引用：12难度：0.8

  解析

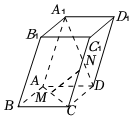• 6．如图，在平行六面体ABCD-A₁B₁C₁D₁中，M在AC上，且AM=

  1

  2

  MC，N在A₁D上，且A₁N=2ND．设

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  MN

  =（　　）

  A．- 1 3 a + 1 3 b + 1 3 c	B． a + 1 3 b - 1 3 c
  C． 1 3 a - 1 3 b - 2 3 c	D．- 1 3 a + b + 1 3 c
  组卷：205引用：6难度：0.8

  解析

• 7．已知F₁，F₂是椭圆

  C

  ：

  x

  2

  25

  +

  y

  2

  16

  =

  1

  的两个焦点，点M在C上，则|MF₁|•|MF₂|的最大值为（　　）

  A．13

  B．12

  C．25

  D．16
  组卷：372引用：3难度：0.7

  解析

四、解答题（共70分）

• 21．已知椭圆的长轴是2

  3

  ，焦点坐标分别是（-

  2

  ，0），（

  2

  ，0）．
  （1）求这个椭圆的标准方程；
  （2）如果直线y=x+m与这个椭圆交于两不同的点，求m的取值范围．
  组卷：28引用：4难度：0.5

  解析

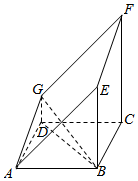• 22．如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
  （Ⅰ）求证：BD⊥平面ADG；
  （Ⅱ）求直线GB与平面AEFG所成角的正弦值．
  组卷：148引用：9难度：0.3

  解析