2022-2023学年湖南省衡阳一中高一（下）期末数学试卷

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若向量

  MN

  =

  （

  a

  ,

  a

  +

  4

  ）

  与

  PQ

  =

  （

  -

  5

  ，

  a

  ）

  垂直，则非零实数a=（　　）

  A．1

  B．2

  C．-1

  D．-2
  组卷：45引用：3难度：0.9

  解析

• 2．“m=4”是“f（x）=（m²-3m-3）x^m+2是幂函数”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：116引用：5难度：0.7

  解析

• 3．已知集合M={0，2，a}，N={2a,4-a}，M∩N≠∅，则a的可能取值的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：71引用：2难度：0.8

  解析

• 4．在正六棱台ABCDEF-A₁B₁C₁D₁E₁F₁中，AB=2，A₁B₁=3，

  A

  A

  1

  =

  10

  ，则该棱台的体积为（　　）

  A． 59 3 4

  B． 59 3 2

  C． 57 3 4

  D． 57 3 2
  组卷：51引用：2难度：0.7

  解析

• 5．将一组互不相等的数据x₁，x₂，…，x₇删去中位数（设中位数为m）后，得到一组新数据，则（　　）

  A．新数据的平均数一定大于原数据的平均数

  B．新数据的平均数一定小于原数据的平均数

  C．新数据的60%分位数一定大于m

  D．新数据的60%分位数一定小于m
  组卷：23引用：2难度：0.8

  解析

• 6．如图，这是一个古典概型的样本空间Ω和事件A，B，其中n（Ω）=120，n（A）=40，n（B）=30，n（A∩B）=10，则（　　）

  A． P （ AB ） = 1 4	B． P （ A ∪ B ） = 1 2
  C．A与B互斥	D．A与B不相互独立
  组卷：136引用：3难度：0.7

  解析

• 7．已知一个圆锥的侧面展开图是半径为4，圆心角为

  π

  2

  的扇形，将该圆锥加工打磨成一个球状零件，则该零件表面积的最大值为（　　）

  A． 12 π 5

  B．2π

  C． 14 π 5

  D． 256 π 15
  组卷：61引用：7难度：0.6

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知函数

  f

  （

  x

  ）

  =

  lg

  4

  x

  ，g（x）=log₂（ax+1）．
  （1）若函数y=1-g（x）在[1，2]内有唯一零点，求a的取值范围．
  （2）设函数φ（x）的最大值、最小值分别为M，m,记D[φ（x）]=M-m.设a=2，函数φ（x）=g（x）-log₂x,当x∈[1，t₁]，

  t

  2

  ∈

  [

  1

  10

  ，

  10

  ]

  时，D[φ（x）]＞D[f（t₂）]恒成立，求t₁的取值范围．
  组卷：41引用：5难度：0.5

  解析

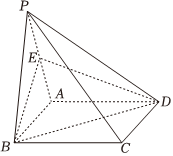• 22．如图，在四棱锥P-ABCD中，底面ABCD是正方形，且AD=2，PA=2，PD=2

  2

  ，∠PAB=60°．
  （1）设平面PAB∩平面PCD=l,证明：l∥CD．
  （2）E是线段PA上的点，且

  PA

  =

  λ

  EA

  （λ＞0），二面角E-BD-A的正切值为

  6

  3

  ，求λ的值．
  组卷：98引用：3难度：0.5

  解析