当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省丹东五中八年级（下）期中数学试卷

发布：2024/7/13 8:0:9

1．2022年北京冬奥会已顺利闭幕，下列历届冬奥会会徽的部分图案中，是中心对称图形的是（　　）
A． B． C． D．
组卷：458引用：17难度：0.8
解析
2．下列各式从左到右的变形中，是因式分解的是（　　）
A．m（a+b+c）=ma+mb+mc B．x²+6x+36=（x+6）²
C．a²-b²+1=（a+b）（a-b）+1 D．10x²-5x=5x（2x-1）
组卷：159引用：3难度：0.6
解析
3．若m＜n,则下列各式中正确的是（　　）
A．-3m＜-3n B．m+1＜n+1 C．3m＞3n D．m-1＞n-1
组卷：63引用：5难度：0.9
解析

4．下列关于等腰三角形的说法错误的是（　　）

A．等腰三角形的角平分线，中线，高线互相重合，简称“三线合一”

B．等腰三角形两底角的平分线相等

C．等腰三角形两腰上的高相等

D．等腰三角形两腰上的中线相等

组卷：132引用：1难度：0.7

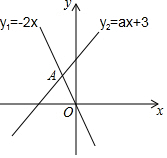5．如图，函数y₁=-2x和y₂=ax+3的图象相交于点A（-1，2），则关于x的不等式-2x＞ax+3的解集是（　　）
A．x＞2 B．x＜2 C．x＞1 D．x＜-1
组卷：571引用：3难度：0.7
解析
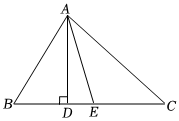6．如图，已知△ABC中，∠B=65°，∠C=45°，AD是BC边上的高，AE是∠BAC的平分线，则∠DAE的度数是（　　）
A．10° B．15° C．25° D．30°
组卷：382引用：4难度：0.5
解析
7．若分式
2
ab
a
+
b
中的a、b的值同时扩大到原来的3倍，则分式的值（　　）
A．不变 B．是原来的3倍
C．是原来的6倍 D．是原来的9倍
组卷：727引用：6难度：0.9
解析
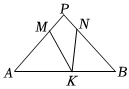8．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=42°，则∠P的度数为（　　）
A．42° B．74° C．84° D．96°
组卷：429引用：3难度：0.5
解析

25．甲、乙两家商场以相同的价格出售同样的商品，为了吸引顾客各自推出不同的优惠方案：在甲商场购买商品超过300元之后，超过部分按8折优惠；在乙商场购买商品超过200元之后，超过部分按8.5折优惠，设甲商场实际付费为y₁元，乙商场实际付费为y₂元，顾客购买商品金额为x元（x＞300）．
（|）分别求出y₁，y₂与x的函数关系式；
（2）比较顾客到哪个商场更优惠，并说明理由．
组卷：76引用：2难度：0.5
解析
26．通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．

原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，试猜想EF、BE、DF之间的数量关系．
（1）思路梳理：
把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，由∠ADG=∠B=90°，得∠FDG=180°，即点F、D、G共线，易证△AFG≌
，故EF、BE、DF之间的数量关系为
．
（2）类比引申：
如图2，点E、F分别在正方形ABCD的边CB、DC的延长线上，∠EAF=45°，连接EF，试猜想EF、BE、DF之间的数量关系为
，并给出证明．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠BAD+∠EAC=45°，若BD=2，EC=2
3
，直接写出AD和DE的长．
组卷：271引用：5难度：0.1
解析