2023-2024学年福建省厦门九中九年级（上）期中数学试卷

一、选择题（共10小题，每题4分，共40分）

• 1．下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的，其中是中心对称图形的是（　　）

  A．	B．
  C．	D．
  组卷：584引用：40难度：0.8

  解析

• 2．在平面直角坐标系中，点（2，-3）关于原点的对称点的坐标是（　　）

  A．（-2，3）

  B．（-2，-3）

  C．（2，3）

  D．（-3，2）
  组卷：486引用：11难度：0.8

  解析

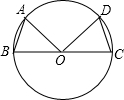• 3．如图，已知在⊙O中，BC是直径，AB=DC，则下列结论不一定成立的是（　　）

  A．OA=OB=AB	B．∠AOB=∠COD
  C． ˆ AB = ˆ DC	D．O到AB、CD的距离相等
  组卷：3280引用：22难度：0.9

  解析

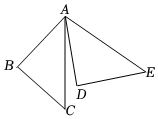• 4．如图，△ADE是由△ABC绕A点旋转得到的，若∠BAC=40°，∠B=90°，∠CAD=10°，则旋转角的度数为（　　）

  A．80°

  B．50°

  C．40°

  D．10°
  组卷：1050引用：17难度：0.8

  解析

• 5．关于x的一元二次方程x²-x+m=0的两个根分别是x₁和x₂，其中

  x

  1

  =

  1

  -

  5

  2

  ，则x₂的值为（　　）

  A． 1 - 5 2

  B． 1 + 5 2

  C．m

  D．-m
  组卷：79引用：1难度：0.5

  解析

• 6．若关于x的一元二次方程x²+4x+c=0有两个不相等的实数根，则c的值可能为（　　）

  A．6

  B．5

  C．4

  D．3
  组卷：2560引用：32难度：0.8

  解析

• 7．在平面直角坐标系中，以原点O为圆心作半径为5的圆，则以下四个点在圆上的是（　　）

  A．（3，0）

  B．（0，6）

  C．（2，4）

  D．（3，4）
  组卷：247引用：2难度：0.5

  解析

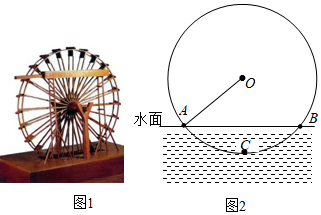• 8．筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且⊙O被水面截得弦AB长为4米，⊙O半径长为3米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（　　）

  A．1米

  B．2米

  C． （ 3 - 5 ） 米

  D． （ 3 + 5 ） 米
  组卷：2077引用：23难度：0.6

  解析

三、解答题（共9题，86分；其中17-21题每题8分，22-23题每题10分，第24题12分，第25题14分）

• 24．△ABC内接于⊙O，AB=AC，∠ABC=67.5°，

  ˆ

  BC

  的长为

  2

  2

  π

  ，点P是射线BC上的动点BP=m（m≥2）．射线OP绕点O逆时针旋转45°得到射线OD，如图所示．点Q是射线OD上的点，点Q与点O不重合，连接PQ，PQ=n.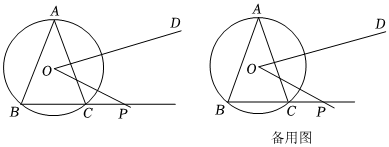
  
  （1）求⊙O的半径；
  （2）当n²=m²-2m+2时，在点P运动的过程中，点Q的位置会随之变化，记Q₁，Q₂是其中任意两个位置，探究直线Q₁Q₂与⊙O的位置关系．
  组卷：583引用：2难度：0.5

  解析

• 25．已知抛物线y=x²+bx+c关于直线x=1对称，且过点（2，1）．
  （1）求抛物线的解析式；
  （2）过D（m,-1）的直线DE：y=k₁x+b₁（k₁＞0）和直线DF：y=k₂x+b₂（k₂＜0）均与抛物线有且只有一个交点．
  ①求k₁k₂的值；
  ②平移直线DE，DF，使平移后的两条直线都经过点R（1，0），且分别与抛物线相交于G、H和P、Q两点，若M、N分别为GH，PQ的中点，求证：直线MN必过某一定点．
  组卷：318引用：4难度：0.3

  解析