2022-2023学年江西省宜春市丰城九中九年级（上）开学数学试卷

一、单选题（本大题共6小题，每小题3分，共18分）

• 1．下列四个银行标志中，是中心对称图形的标志是（　　）

  A．

  B．

  C．

  D．
  组卷：60引用：3难度：0.9

  解析

• 2．若P（x,3）与点Q（4，y）关于原点对称，则xy的值是（　　）

  A．12

  B．-12

  C．64

  D．-64
  组卷：816引用：14难度：0.7

  解析

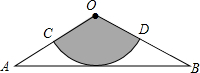• 3．如图，从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面半径为（　　）

  A．15cm

  B．12cm

  C．10cm

  D．20cm
  组卷：2901引用：25难度：0.8

  解析

• 4．如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AC=12，AE=3，则⊙O的直径长为（　　）

  A．10

  B．13

  C．15

  D．16
  组卷：4318引用：15难度：0.5

  解析

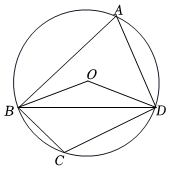• 5．如图，四边形ABCD内接于⊙O，连接OB，OD，BD，若∠C=110°，则∠OBD=（　　）

  A．15°

  B．20°

  C．25°

  D．30°
  组卷：2093引用：16难度：0.7

  解析

• 6．将△OBA按如图方式放在平面直角坐标系中，其中∠OBA=90°，∠A=30°，顶点A的坐标为（1，

  3

  ），将△OBA绕原点逆时针旋转，每次旋转60°，则第2023次旋转结束时，点A对应点的坐标为（　　）

  A． （ - 1 ， 3 ）

  B． （ - 3 ， 1 ）

  C． （ - 3 3 ， 1 ）

  D． （ - 1 ， 3 3 ）
  组卷：627引用：5难度：0.4

  解析

二、填空题（本大题共6小题，每小题3分，共18分）

• 7．用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是

  ．
  组卷：2566引用：84难度：0.7

  解析

五、（本大题共2小题，每小题9分，共18分）

• 22．在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
  （1）点C的坐标是

  ，△ABC的面积是

  ；
  （2）将△ABC绕点C旋转180°得到△A₁B₁C₁，连接AB₁、BA₁，画出四边形AB₁A₁B，并判断四边形AB₁A₁B是何种特殊四边形

  ；
  （3）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．
  组卷：27引用：3难度：0.5

  解析

六、（本大题共12分）

• 23．在等边三角形ABC中，点D在射线BC上（不与点B，C重合），把线段AD绕点D顺时针旋转60°，得到线段DE，连接CE．
  （1）当点D在BC边上时，如图1，∠ACE的度数是

  ；
  BD与CE之间的数量关系

  ．
  （2）当点D在BC边的延长线上时，如图2，（1）中的两个结论是否仍然成立？如果成立，请就图②情形进行证明；若不成立，请说明理由．
  （3）若AB=4，当∠DEC=30°，请直接写出线段BD的长．
  
  组卷：115引用：6难度：0.2

  解析