2022-2023学年湖南省常德市桃源一中高三(上)期中数学试卷
发布:2024/9/5 0:0:8
一、单选题(本题共8个小题,每小题5分,共40分)
-
1.已知集合A={x∈Z|x2+x>6},B={x|-4≤x≤4},则A∩B=( )
组卷:163引用:3难度:0.8 -
2.已知复数z满足:(2+i)z=m,(其中i为虚数单位,m为实数且m<0),则z的共轭复数
在复平面内对应的点位于( )z组卷:59引用:4难度:0.7 -
3.直线l:ax+(1-a)y+1=0经过第一象限的充要条件是( )
组卷:2引用:1难度:0.7 -
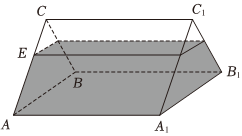 4.如图,一个直三棱柱形容器中盛有水,且侧棱AA1=4.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的四等分点处,,当底面ABC水平放置时,液面高为( )CECA=14组卷:30引用:7难度:0.4
4.如图,一个直三棱柱形容器中盛有水,且侧棱AA1=4.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的四等分点处,,当底面ABC水平放置时,液面高为( )CECA=14组卷:30引用:7难度:0.4 -
5.在平面直角坐标系中,已知点P(3,4)为角α终边上一点,若
,β∈(0,π),则sinβ=( )cos(α+β)=13组卷:53引用:6难度:0.6 -
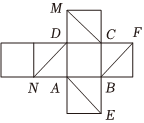 6.如图是正方体的平面展开图,在这个正方体中,下列判断不正确的是( )组卷:6引用:2难度:0.8
6.如图是正方体的平面展开图,在这个正方体中,下列判断不正确的是( )组卷:6引用:2难度:0.8 -
7.已知函数f(x)的定义域为R,函数g(x)=f(x)+x2为奇函数,且g(x+4)=g(x),则f(6)的值为( )
组卷:447引用:2难度:0.7
四、解答题(本题共6个小题,共70分)
-
21.已知函数f(x)=xlnx-ax2+3x.
(1)若对任意的x∈(0,+∞),f(x)≤1恒成立,求实数a的取值范围;
(2)证明:当n∈N*时,.31×2+42×3+53×4+…+n+2n(n+1)≥ln(n+1)组卷:159引用:4难度:0.5 -
22.已知函数f(x)=ln(2x+1)+2ax-4aex+4,其中a>0
(1)当a=1时,求f(x)的最大值;
(2)判断函数f(x)零点的个数,并说明理由.组卷:23引用:3难度:0.7


