当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省泰州市高港区口岸中学高一（下）第一次段考数学试卷

发布：2024/7/11 8:0:9

一、单项选择题（本大题共8小题，每小题5分，共40分）

1．已知向量
a
=
（
1
，-
2
）
，
b
=
（
m
,
4
）
，且
a
∥
b
，那么
a
-
b
等于（　　）
A．（4，0） B．（0，4） C．（3，-6） D．（-3，6）
组卷：135引用：5难度：0.8
解析
2．已知
a
、
b
均为单位向量，它们的夹角为60°，那么|
a
+
3
b
|=（　　）
A．
7
B．
10
C．
13
D．4
组卷：1507引用：137难度：0.9
解析
3．sin400°cos20°-cos40°cos110°=（　　）
A．
1
2
B．
-
1
2
C．
3
2
D．
-
3
2
组卷：739引用：3难度：0.7
解析
4．八角星纹是大汶口文化中期彩陶纹样中具有鲜明特色的花纹．八角星纹常绘于彩陶盆和豆的上腹，先于器外的上腹施一圈红色底衬，然后在上面绘并列的八角星形的单独纹样．八角星纹以白彩的成，黑线勾边，中为方形或圆形，且有向四面八方扩张的感觉．八角星纹延续的时间较长，传播范围亦广，在长江以南的时间稍晚的崧泽文化的陶豆座上也屡见刻有八角大汶口文化八角星纹．图2是图1抽象出来的图形，在图2中，圆中各个三角形（如△ACD）为等腰直角三角形，点O为圆心，中间部分是正方形且边长为2，定点A，B所在位置如图所示，则
AB
•
AO
的值为（　　）
A．10 B．12 C．14 D．16
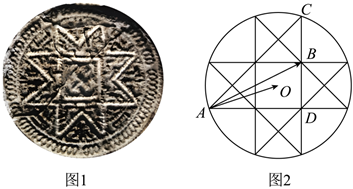组卷：353引用：9难度：0.6
解析
5．已知向量
a
=
（
1
，
1
）
，
b
=
（
1
，
0
）
，则
a
在
b
上的投影向量的模为（　　）
A．2 B．
3
C．1 D．
3
3
组卷：45引用：2难度：0.9
解析
6．已知
a
，
b
满足
|
b
|
=
2
，
b
与
b
-
a
的夹角为120°，记
m
=
t
a
+
（
1
-
t
）
b
，则
|
m
|
的最小值为（　　）
A．
3
B．
2
C．1 D．
1
2
组卷：45引用：2难度：0.7
解析
7．已知
-
π
2
＜
β
-
α
＜
π
2
，sinβ-2cosα=1，
2
sinα
+
cosβ
=
2
，则
cos
（
α
-
π
3
）
=（　　）
A．
±
6
3
B．
±
3
3
C．
3
3
D．
6
3
组卷：729引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分.解答时应写出文字说明、证明过程或演算步骤）

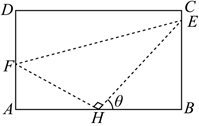21．如图，某污水处理厂要在一个矩形污水处理池ABCD的池底水平铺设污水净化管道（Rt△FHE三条边）来处理污水，管道越长，污水净化效果越好．要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上（含线段两端点），已知
AB
=
30
3
米，AD=45米，∠BHE=θ．
（1）设Rt△FHE的周长为L，求L关于θ的函数关系式，并求出定义域；
（2）θ为何值时，污水净化效果最好？
组卷：15引用：3难度：0.4
解析
22．已知向量
a
=（cos
3
x
2
，sin
3
x
2
），
b
=（cos
x
2
，-sin
x
2
），函数f（x）=
a
•
b
-m|
a
+
b
|+1，
x
∈
[
-
π
3
，
π
4
]
，
m
∈
R
．
（1）若f（x）的最小值为-1，求实数m的值；
（2）是否存在实数m,使函数
g
（
x
）
=
f
（
x
）
+
24
49
m
2
，
x
∈
[
-
π
3
，
π
4
]
有四个不同的零点？若存在，求出m的取值范围；若不存在，请说明理由．
组卷：197引用：11难度：0.5
解析