2022-2023学年江苏省无锡市滨湖区金桥双语实验学校八年级（上）期中数学试卷
发布：2024/9/15 13:0:8
一．选择题（共10小题）
-
1．2022年冬奥会将在北京举行，中国将是第一个实现奥运“全满贯”（先后举办奥运会、残奥会、青奥会、冬奥会、冬残奥会）的国家．以下会徽是轴对称图形的是（ ）
组卷：310引用：15难度：0.9 -
2．下列计算正确的是（ ）
组卷：263引用：4难度：0.8 -
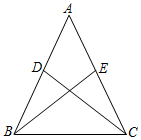3．如图，在△ABC中，AB=AC，D、E两点分别在边AB、AC上．添加一个条件，仍不能判定△ABE≌△ACD，则这个条件是（ ）组卷：62引用：2难度：0.7 -
4．下列命题中正确的是（ ）
组卷：234引用：4难度：0.7 -
5．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图，一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的平分线．”他这样做的依据是（ ）组卷：582引用：19难度：0.5 -
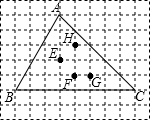6．在正方形网格中，△ABC的位置如图所示，且顶点在格点上，在△ABC内部有E、F、G、H四个格点，到△ABC三个顶点距离相等的点是（ ）组卷：2092引用：22难度：0.8 -
7．如图，已知△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为1，l2，l3之间的距离为2，则AC2=（ ）组卷：551引用：10难度：0.7 -
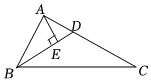8．如图，在△ABC中，BD为∠ABC的平分线，AE⊥BD，垂足为E，且AB=5，AE=3，BC=11，则∠BAE与∠C的关系为（ ）组卷：693引用：3难度：0.9 -
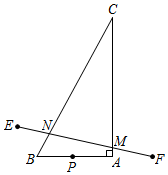9．如图，Rt△ABC中，∠A=90°，∠C=30°，AB=1，AC=，动点P在边AB上（不与A、B重合），点P关于BC，AC的对称点分别为点E，F，连接EF，交AC，BC分别为点M，N．3
甲：我发现线段EF的最大值为2，最小值为；3
乙：我连接PM，PN，发现△PMN一定为钝角三角形．
则下列判断正确的是（ ）组卷：365引用：4难度：0.6
三．解答题
-
26．若△ABC和△ADE均为等腰三角形，且AB=AC=AD=AE，当∠ABC和∠ADE互余时，称△ABC与△ADE互为“底余等腰三角形”，△ABC的边BC上的高AH叫做△ADE的“余高”．
（1）如图1，△ABC与△ADE互为“底余等腰三角形”．
①若连接BD，CE，判断△ABD与△ACE是否互为“底余等腰三角形”：（填“是”或“否”）；
②当∠BAC=90°时，若△ADE的“余高”AH=，则DE=；5
③当0°＜∠BAC＜180°时，判断DE与AH之间的数量关系，并证明；
（2）如图2，在四边形ABCD中，∠ABC=60°，DA⊥BA，DC⊥BC，且DA=DC．
①画出△OAB与△OCD，使它们互为“底余等腰三角形”；
②若△OCD的“余高”长为a,则点A到BC的距离为 （用含a的式子表示）．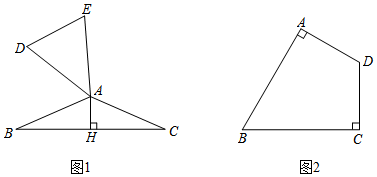
组卷：652引用：5难度：0.3 -
27．小明在一次数学兴趣小组活动中，对一个数学问题做如下探究：
【问题背景】
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC、BC、CD之间的数量关系．小明同学探究此问题的思路是：将△BCD绕点D逆时针旋转90°到△AED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=CD，从而得出结论：AC+BC=CD．2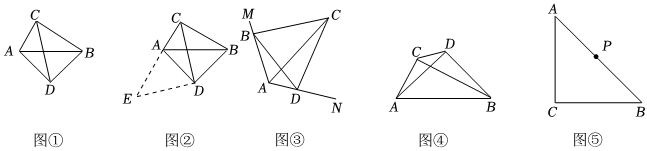
【简单应用】
（1）在图①中，若AB=5，BC=4，则CD2=．
（2）如图③，在四边形ABCD中，∠BAD=120°，点B和点D分别在边AM和AN上移动，且满足∠BCD与∠BAD互补，CB=CD，AC=6，则以下结论：
①AB+AD的值不变；
②∠BAC=∠DAC恒成立；
③BD的长不变；
④四边形ABCD的面积不变，其中正确的序号有 ．
【拓展延伸】
（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=a,BC=b（a＜b），求CD2的长．（用含a、b的代数式表示）．
（4）如图⑤，∠ACB=90°，AC=BC=13，点P为AB的中点，若点E满足AE=10，CE=CA，点Q为AE的中点，则PQ2=．组卷：436引用：1难度：0.3
