2022-2023学年浙江省台州市八校联盟高二（上）期中数学试卷

一、单项选择题：本大题共8小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知直线l的方程为

  3

  x

  +

  y

  -

  2

  =

  0

  ，则直线的倾斜角为（　　）

  A．-30°

  B．60°

  C．120°

  D．150°
  组卷：57引用：9难度：0.7

  解析

• 2．圆x²-8x+y²+12=0与圆x²+y²-6y-7=0的位置关系是（　　）

  A．相离

  B．相交

  C．内切

  D．外切
  组卷：34引用：3难度：0.7

  解析

• 3．如图，在平行六面体ABCD-A₁B₁C₁D₁中，E为A₁C₁的中点，若

  BE

  =

  x

  AA

  1

  +

  y

  AB

  +

  z

  AD

  ，则（　　）

  A．x=1，y= 1 2 ，z=- 1 2	B．x=1，y=- 1 2 ，z= 1 2
  C．x= 1 2 ，y=1，z=- 1 2	D．x=- 1 2 ，y=1，z= 1 2
  组卷：253引用：16难度：0.7

  解析

• 4．如果AB＜0，BC＜0，那么直线Ax-By-C=0不经过（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：100引用：12难度：0.9

  解析

• 5．设x,y∈R，向量

  a

  =

  （

  0

  ，

  1

  ，

  z

  ）

  ，

  b

  =

  （

  2

  ，

  y

  ,

  2

  ）

  ，

  c

  =

  （

  -

  3

  ，

  6

  ，-

  3

  ）

  ，且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，则

  |

  a

  -

  b

  |

  =（　　）

  A． 29

  B． 2 6

  C．3

  D． 2 2
  组卷：78引用：11难度：0.7

  解析

• 6．在两坐标轴上的截距相等，且与圆（x-3）²+（y-4）²=2相切的直线有（　　）条

  A．1

  B．2

  C．3

  D．4
  组卷：44引用：3难度：0.8

  解析

• 7．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，

  O

  为椭圆的对称中心，F为椭圆的一个焦点，P为椭圆上一点，PF⊥x轴，PF与椭圆的另一个交点为点Q，△POQ为等腰直角三角形，则椭圆的离心率为（　　）

  A． 3 2

  B． 5 - 1 2

  C． 3 + 1 4

  D． 3 5
  组卷：117引用：9难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．在斜三棱柱ABC-A₁B₁C₁中，△ABC为等腰直角三角形，AB=AC，侧面BB₁C₁C为菱形，且∠B₁BC=60°，点E为棱A₁A的中点，EB₁=EC，平面B₁CE⊥平面BB₁C₁C．
  
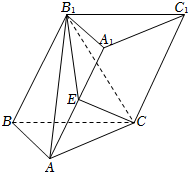
  （1）证明：平面BB₁C₁C⊥平面ABC；
  （2）求平面AB₁C与平面B₁CE的夹角的余弦值．
  组卷：109引用：4难度：0.6

  解析

• 22．已知点P与定点

  F

  （

  3

  ，

  0

  ）

  的距离和它到定直线

  x

  =

  4

  3

  3

  的距离比是

  3

  2

  ．
  （1）求点P的轨迹方程C；
  （2）若直线y=kx+m与轨迹C交于M，N两点，O为坐标原点直线OM，ON的斜率之积等于

  -

  1

  4

  ，试探求△OMN的面积是否为定值，并说明理由．
  组卷：86引用：6难度：0.5

  解析