当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙市A佳教育联盟高三（下）月考数学试卷（4月份）

发布：2024/7/22 8:0:9

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合
A
=
{
x
|
x
-
1
x
+
3
＜
0
}
，
B
=
{
x
|
y
=
ln
（
1
-
2
x
）
}
，则A∩B=（　　）
A．（-3，1） B．
（
1
2
，
1
）
C．
（
-
3
，
1
2
）
D．
（
-
1
2
，
1
）
组卷：29引用：2难度：0.7
解析
2．已知复数z满足（1+2i）z=2+i,则复数
z
在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：32引用：4难度：0.8
解析
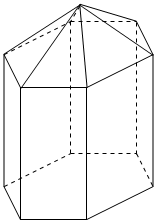3．为了给热爱朗读的师生提供一个安静独立的环境，某学校修建了若干“朗读亭”．如图所示，该朗读亭的外形是一个正六棱柱和正六棱锥的组合体，正六棱柱两条相对侧棱所在的轴截面为正方形，若正六棱锥的高与底面边长的比为2：3，则正六棱锥与正六棱柱的侧面积的比值为（　　）
A．
7
8
B．
43
24
C．
1
9
D．
1
27
组卷：59引用：2难度：0.7
解析
4．建筑学中必须要对组合墙的平均隔声量进行设计．组合墙是指带有门或窗等的隔墙，假定组合墙上有门、窗及孔洞等几种不同的部件，隔墙及各种部件的面积分别为S₁，S₂，⋯，S_n（单位：m²），其相应的透射系数分别为τ₁，τ₂，⋯，τ_n，则组合墙各部分的透射系数的平均值
τ
为：
τ
=
S
1
τ
1
+
S
2
τ
2
+
⋯
+
S
n
τ
n
S
1
+
S
2
+
⋯
+
S
n
，于是组合墙的平均隔声量（单位：dB）可用公式：
R
=
10
lg
1
2
τ
估算而得．已知某墙的透射系数为
1
10
4
，面积为20m²，在墙上有一扇门和窗，门的透射系数为
1
10
2
，面积为2m²，窗的透射系数为
1
10
3
，面积为3m²，则组合墙的平均隔声量约为（　　）dB．（注：lg2≈0.3010，lg3≈0.4771）
A．18.322 B．26.990 C．33.010 D．44.302
组卷：33引用：2难度：0.5
解析
5．在平面四边形ABCD中，
AD
•
CD
=
0
，
|
AB
|
=
|
AD
|
=
1
，
AD
•
AB
=
-
1
2
，
|
CD
|
=
3
，若点E为线段CD上的动点，则
AE
•
BE
的取值范围为（　　）
A．
[
3
2
，
3
]
B．
[
3
2
，
21
16
]
C．
[
21
16
，
3
]
D．
[
3
，
2
3
]
组卷：36引用：2难度：0.6
解析
6．已知函数f（x）=sin（ωx+φ）（0＜ω＜3，|φ|＜π），且
f
（
-
π
3
）
-
f
（
2
π
3
）
=
2
，则当
f
（
α
）
=
1
4
时，
cos
（
2
α
+
2
π
3
）
=（　　）
A．
-
15
8
B．
15
8
C．
-
7
8
D．
7
8
组卷：41引用：2难度：0.6
解析
7．数列{a_n}的前n项和为S_n，满足
S
n
+
1
+
S
n
-
1
=
2
S
n
-
a
2
n
（
n
≥
2
）
，
a
1
∈
（
1
2
，
1
）
，则下列结论中错误的是（　　）
A．0＜a_n+1＜a_n B．
n
∑
i
=
1
a
2
i
＜
1
C．
n
＜
n
∑
i
=
1
1
1
-
a
i
＜
2
n
D．
a
n
＞
1
n
+
2
组卷：53引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．已知双曲线
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右顶点为A，过右焦点F的直线与C交于P，Q两点．当PQ⊥x轴时，
|
PA
|
=
10
，
△
PAQ
的面积为3．
（1）求双曲线C的方程；
（2）过点T（t,0）（-1＜t＜1）的直线l与曲线C交于点M，N（异于点A），直线MA，NA与直线x=t分别交于点G，H．若点F，A，G，H四点共圆，求实数t的值．
组卷：82引用：2难度：0.5
解析
22．设函数
f
（
x
）
=
1
+
alnx
x
，其中a≥0．
（1）讨论函数f（x）的单调性；
（2）已知f（x）有极大值为1，设h（x）=x²[1-f（x）]+x-1，若m＞0，n＞0，且mn＞1，证明：h（m）+h（n）＞0．
组卷：47引用：2难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．0＜a_n+1＜a_n	B． n ∑ i = 1 a 2 i ＜ 1
C． n ＜ n ∑ i = 1 1 1 - a i ＜ 2 n	D． a n ＞ 1 n + 2

2022-2023学年湖南省长沙市A佳教育联盟高三（下）月考数学试卷（4月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合A={x|x-1x+3＜0}，B={x|y=ln（1-2x）}，则A∩B=（ ）

2．已知复数z满足（1+2i）z=2+i,则复数z在复平面内对应的点位于（ ）

5．在平面四边形ABCD中，AD•CD=0，|AB|=|AD|=1，AD•AB=-12，|CD|=3，若点E为线段CD上的动点，则AE•BE的取值范围为（ ）

6．已知函数f（x）=sin（ωx+φ）（0＜ω＜3，|φ|＜π），且f（-π3）-f（2π3）=2，则当f（α）=14时，cos（2α+2π3）=（ ）

7．数列{an}的前n项和为Sn，满足Sn+1+Sn-1=2Sn-a2n（n≥2），a1∈（12，1），则下列结论中错误的是（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

22．设函数f（x）=1+alnxx，其中a≥0．（1）讨论函数f（x）的单调性；（2）已知f（x）有极大值为1，设h（x）=x2[1-f（x）]+x-1，若m＞0，n＞0，且mn＞1，证明：h（m）+h（n）＞0．

1．已知集合
A
=
{
x
|
x
-
1
x
+
3
＜
0
}
，
B
=
{
x
|
y
=
ln
（
1
-
2
x
）
}
，则A∩B=（　　）

2．已知复数z满足（1+2i）z=2+i,则复数
z
在复平面内对应的点位于（　　）

5．在平面四边形ABCD中，
AD
•
CD
=
0
，
|
AB
|
=
|
AD
|
=
1
，
AD
•
AB
=
-
1
2
，
|
CD
|
=
3
，若点E为线段CD上的动点，则
AE
•
BE
的取值范围为（　　）

6．已知函数f（x）=sin（ωx+φ）（0＜ω＜3，|φ|＜π），且
f
（
-
π
3
）
-
f
（
2
π
3
）
=
2
，则当
f
（
α
）
=
1
4
时，
cos
（
2
α
+
2
π
3
）
=（　　）

7．数列{a_n}的前n项和为S_n，满足
S
n
+
1
+
S
n
-
1
=
2
S
n
-
a
2
n
（
n
≥
2
）
，
a
1
∈
（
1
2
，
1
）
，则下列结论中错误的是（　　）

22．设函数
f
（
x
）
=
1
+
alnx
x
，其中a≥0．
（1）讨论函数f（x）的单调性；
（2）已知f（x）有极大值为1，设h（x）=x²[1-f（x）]+x-1，若m＞0，n＞0，且mn＞1，证明：h（m）+h（n）＞0．