2021-2022学年四川省内江市隆昌七中高二（下）期中数学试卷（文科）

一、选择题：本题共12小题，每小题5分，共60分。

• 1．已知焦点在x轴上的椭圆

  x

  2

  m

  +

  y

  2

  9

  =1的离心率e=

  1

  2

  ，则m=（　　）

  A．12

  B．18

  C． 27 4

  D．12或 27 4
  组卷：28引用：2难度：0.9

  解析

• 2．设x∈R，则“x²-3x＜0”是“1＜x＜2”的（　　）

  A．充要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：707引用：11难度：0.8

  解析

• 3．若方程x²+ky²=2表示焦点在y轴上的椭圆，那么实数k的取值范围是（　　）

  A．（0，+∞）

  B．（0，2）

  C．（1，+∞）

  D．（0，1）
  组卷：5057引用：140难度：0.9

  解析

• 4．如果椭圆

  x

  2

  36

  +

  y

  2

  9

  =1的弦被点（4，2）平分，则这条弦所在的直线方程是（　　）

  A．x-2y=0

  B．x+2y-4=0

  C．2x+3y-12=0

  D．x+2y-8=0
  组卷：847引用：91难度：0.9

  解析

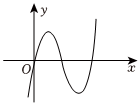• 5．设函数y=f（x）的图象如图，则导函数y=f′（x）的图象可能是图中的（　　）
  ​

  A．

  B．

  C．

  D．​
  组卷：41引用：2难度：0.6

  解析

• 6．下列函数求导运算正确的个数为（　　）
  ①（3^x）′=3^xlog₃e；
  ②（log₂x）′=

  1

  xln

  2

  
  ③（e^x）′=e^x；
  ④（

  1

  lnx

  ）′=x；
  ⑤（x•e^x）′=e^x+1．

  A．1

  B．2

  C．3

  D．4
  组卷：354引用：28难度：0.9

  解析

• 7．函数y=x³-3x²-9x（-2＜x＜2）有（　　）

  A．极大值5，极小值-27	B．极大值5，极小值-11
  C．极大值5，无极小值	D．极小值-27，无极大值
  组卷：398引用：106难度：0.9

  解析

三、解答题（本大题共6小题；共70分，解答应写出文字说明、证明过程或演算步骤）

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  1

  2

  ，M是椭圆C的上顶点，F₁，F₂是椭圆C的焦点，△MF₁F₂的周长是6．
  （1）求椭圆C的标准方程；
  （2）过动点P（1，t）作直线交椭圆C于A，B两点，且|PA|=|PB|，过P作直线l,使l与直线AB垂直，证明：直线l恒过定点，并求此定点的坐标．
  组卷：26引用：1难度：0.3

  解析

• 22．已知函数f（x）=

  lnx

  +

  a

  x

  （a∈R）．
  （1）若曲线y=f（x）在点（1，f（1））处的切线与直线x-y-1=0平行，求a的值；
  （2）在（1）条件下，求函数f（x）的单调区间和极值；
  （3）当a=1，且x≥1时，证明：f（x）≤1．
  组卷：53引用：5难度：0.5

  解析