2022-2023学年江西省宜春市宜丰中学创新部高二（下）期末数学试卷

一、单选题

• 1．直线mx+ny+3=0在y轴上的截距为-3，而且它的斜率是直线

  3

  x-y=3

  3

  的斜率的相反数，则（　　）

  A．m=- 3 ，n=1

  B．m=- 3 ，n=-3

  C．m=- 3 ，n=-1

  D．m= 3 ，n=1
  组卷：325引用：3难度：0.7

  解析

• 2．已知

  C

  m

  8

  =

  C

  2

  m

  -

  1

  8

  ，则m等于（　　）

  A．1

  B．3

  C．1或3

  D．1或4
  组卷：592引用：10难度：0.7

  解析

• 3．从某班包含甲、乙的5名班干部中选出3人参加学校的社会实践活动，在甲被选中的情况下，乙也被选中的概率为（　　）

  A． 1 2

  B． 3 5

  C． 2 3

  D． 2 5
  组卷：528引用：4难度：0.8

  解析

• 4．若直线l₁：ax+3y+2=0与直线l₂：x-（a+1）y+a=0垂直，则实数a=（　　）

  A．0

  B．1

  C． - 3 4

  D． - 3 2
  组卷：205引用：4难度：0.8

  解析

• 5．一堆苹果中大果与小果的比例为9：1，现用一台水果分选机进行筛选．已知这台分选机把大果筛选为小果的概率为5%，把小果筛选为大果的概率为2%．经过一轮筛选后，现在从这台分选机筛选出来的“大果”里面随机抽取一个，则这个“大果”是真的大果的概率为（　　）

  A． 855 857

  B． 857 1000

  C． 171 200

  D． 9 10
  组卷：452引用：8难度：0.8

  解析

• 6．在正四棱柱ABCD-A₁B₁C₁D₁中，

  AB

  =

  BC

  =

  3

  ，

  A

  A

  1

  =

  1

  ，则异面直线AD₁与DB₁所成角的余弦值为（　　）

  A． 5 5

  B． 2 5 5

  C． 7 7

  D． - 7 7
  组卷：155引用：6难度：0.6

  解析

• 7．抛物线C：y²=8x的焦点为F，准线为l,点P是准线l上的动点，若点A在抛物线C上，且|AF|=10，则|PA|+|PO|（O为坐标原点）的最小值为（　　）

  A． 13

  B．2 13

  C．3 13

  D．4 13
  组卷：180引用：3难度：0.6

  解析

四、解答题

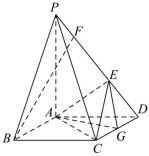• 21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是边长为2的正方形，PA=2，G为CD的中点，E，F是棱PD上两点（F在E的上方），且EF=

  2

  ．
  （1）若DE=

  2

  2

  ，求证：BF∥平面AEG；
  （2）当点F到平面AEC的距离取得最大值时，求DE的长．
  组卷：189引用：3难度：0.3

  解析

• 22．已知椭圆C的左、右焦点分别为F₁，F₂，焦距为2，点

  P

  （

  1

  ，

  3

  2

  ）

  在椭圆C上．
  （1）求椭圆C的标准方程；
  （2）已知M是直线l：x=t上的一点，是否存在这样的直线l,使得过点M的直线与椭圆C相切于点N，且以MN为直径的圆过点F₂？若存在，求出直线l的方程；若不存在，说明理由．
  组卷：19引用：2难度：0.5

  解析