当前位置：试卷中心 > 试卷详情

2023-2024学年湖北省武汉市武昌实验中学高三（上）月考数学试卷（10月份）

发布：2024/9/11 2:0:8

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若集合M={x|log₂x＜4}，N={x|2x≥1}，则M∩N=（　　）
A．{x|0≤x＜8} B．
{
x
|
1
2
≤
x
＜
8
}
C．{x|2≤x＜16} D．
{
x
|
1
2
≤
x
＜
16
}
组卷：141引用：10难度：0.7
解析
2．若复数z=1-i+i²-i³+⋯+i²⁰²²-i²⁰²³，则|z|=（　　）
A．0 B．
2
C．1 D．2
组卷：168引用：5难度：0.8
解析
3．记等差数列{a_n}的前n项和为S_n，若a₆=16，S₅=35，则{a_n}的公差为（　　）
A．-3 B．-2 C．3 D．2
组卷：632引用：10难度：0.6
解析

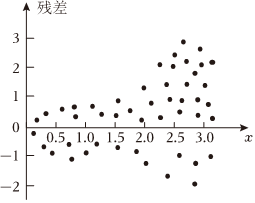4．根据变量Y和x的成对样本数据，用一元线性回归模型
Y
=
bx
+
a
+
e
E
（
e
）
=
0
，
D
（
e
）
=
σ
2
得到经验回归模型
̂
y
=
̂
b
x
+
̂
a
，对应的残差如图所示，模型误差（　　）

A．满足一元线性回归模型的所有假设

B．不满足一元线性回归模型的E（e）=0的假设

C．不满足一元线性回归模型的D（e）=σ²假设

D．不满足一元线性回归模型的E（e）=0和D（e）=σ²的假设

组卷：314引用：7难度：0.6

解析

5．已知椭圆
C
：
x
2
16
+
y
2
12
=
1
的左、右焦点分别为F₁，F₂，点P是椭圆C上的动点，m=|PF₁|，n=|PF₂|，则
4
m
+
n
mn
的最小值为（　　）
A．
9
8
B．
5
4
C．
20
-
3
7
9
D．
20
+
3
7
9
组卷：365引用：4难度：0.6
解析
6．我国南宋著名数学家秦九韶发现了“三斜”求积公式，即△ABC的三个内角A，B，C所对的边分别为a,b,c,则△ABC的面积S=
1
4
[
a
2
c
2
-
（
a
2
+
c
2
-
b
2
2
）
2
]
，若b=
2
，
a
+
b
+
c
sin
A
+
sin
B
+
sin
C
=
c
2
sin
A
，则△ABC面积S的最大值为（　　）
A．
2
B．1 C．
2
3
D．
2
3
组卷：18引用：6难度：0.6
解析

7．某人在n次射击中击中目标的次数为X，X～B（n,p），其中n∈N^*，0＜p＜1，击中奇数次为事件A，则（　　）

A．若n=10，p=0.8，则P（X=k）取最大值时k=9

B．当

时，D（X）取得最小值

C．当

＜

时，P（A）随着n的增大而增大

D．当

＜

时，P（A）随着n的增大而减小

组卷：326引用：4难度：0.4

解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

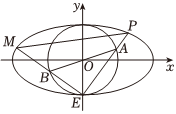21．在△PF₁F₂中，已知点
F
1
（
-
3
，
0
）
，
F
2
（
3
，
0
）
，
P
F
1
与PF₂边上的中线长之和为6．记△PF₁F₂的重心G的轨迹为曲线C．
（1）求C的方程；
（2）若圆O：x²+y²=1，E（0，-1），过坐标原点O且与y轴不重合的任意直线l与圆O相交于点A，B，直线EA，EB与曲线C的另一个交点分别是点P，M，求△EPM面积的最大值．
组卷：48引用：12难度：0.5
解析
22．人口老龄化加剧的背景下，我国先后颁布了一系列生育政策，根据不同政策要求，分为两个时期Ⅰ和Ⅱ．根据部分调查数据总结出如下规律：
对于同一个家庭，在Ⅰ时期内生孩X人，在Ⅱ时期生孩Y人，（不考虑多胞胎）生男生女的概率相等．X服从0-1分布且P（x=0）=
1
5
．Y分布列如下：

Y 0 1 2

P p p+q p-q

现已知一个家庭在Ⅰ时期没生孩子，则在Ⅱ时期生2个孩子概率为
1
24
；若在Ⅰ时期生了1个女孩，则在时期生2个孩子概率为
1
6
；若在Ⅰ时期生了1个男，则在Ⅱ时期生2个孩子概率为
1
12
，样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为2：5（针对普遍家庭）．
（1）求Y的期望与方差；
（2）由数据z_i（i=1，2，…，n）组成的样本空间根据分层随机抽样分为两层，样本点之比为a：b,分别为x_i（i=1，2，…，k）与y_i（i=1，2，…，m），k+m=n,总体本点与两个分层样本点均值分别为
z
，
x
，
y
，方差分别为
s
2
0
，
s
2
1
，
s
2
2
，证明：
s
2
0
=
a
a
+
b
[
s
2
1
+
（
x
-
z
）
2
]
+
b
a
+
b
[
s
2
2
+
（
y
-
z
）
2
]
，并利用该公式估算题设样本总体的方差．
组卷：118引用：4难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

Y	0	1	2
P	p	p+q	p-q

2023-2024学年湖北省武汉市武昌实验中学高三（上）月考数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若集合M={x|log2x＜4}，N={x|2x≥1}，则M∩N=（ ）

2．若复数z=1-i+i2-i3+⋯+i2022-i2023，则|z|=（ ）

3．记等差数列{an}的前n项和为Sn，若a6=16，S5=35，则{an}的公差为（ ）

4．根据变量Y和x的成对样本数据，用一元线性回归模型Y=bx+a+eE（e）=0，D（e）=σ2得到经验回归模型̂y=̂bx+̂a，对应的残差如图所示，模型误差（ ）

5．已知椭圆C：x216+y212=1的左、右焦点分别为F1，F2，点P是椭圆C上的动点，m=|PF1|，n=|PF2|，则4m+nmn的最小值为（ ）

6．我国南宋著名数学家秦九韶发现了“三斜”求积公式，即△ABC的三个内角A，B，C所对的边分别为a,b,c,则△ABC的面积S=14[a2c2-（a2+c2-b22）2]，若b=2，a+b+csinA+sinB+sinC=c2sinA，则△ABC面积S的最大值为（ ）

7．某人在n次射击中击中目标的次数为X，X～B（n,p），其中n∈N*，0＜p＜1，击中奇数次为事件A，则（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

1．若集合M={x|log₂x＜4}，N={x|2x≥1}，则M∩N=（　　）

2．若复数z=1-i+i²-i³+⋯+i²⁰²²-i²⁰²³，则|z|=（　　）

3．记等差数列{a_n}的前n项和为S_n，若a₆=16，S₅=35，则{a_n}的公差为（　　）

4．根据变量Y和x的成对样本数据，用一元线性回归模型
Y
=
bx
+
a
+
e
E
（
e
）
=
0
，
D
（
e
）
=
σ
2
得到经验回归模型
̂
y
=
̂
b
x
+
̂
a
，对应的残差如图所示，模型误差（　　）

5．已知椭圆
C
：
x
2
16
+
y
2
12
=
1
的左、右焦点分别为F₁，F₂，点P是椭圆C上的动点，m=|PF₁|，n=|PF₂|，则
4
m
+
n
mn
的最小值为（　　）

7．某人在n次射击中击中目标的次数为X，X～B（n,p），其中n∈N^*，0＜p＜1，击中奇数次为事件A，则（　　）